username@email.com
username@email.com
In this lesson, we’ll discuss mathematical reasoning and methods of problem solving with an eye toward helping your students make the best use of their reasoning skills when it comes to tackling complex problems.
When solving a mathematical problem, it is very common for a student to feel overwhelmed by the information or lack a clear idea about how to get started.
To help the students with their problem-solving “problem,” let’s look at some examples of mathematical problems and some general methods for solving problems:
Identify the following four-digit number when presented with the following information:
Help your students identify and prioritize the information presented.
In this particular example, we want to look for concrete information. Clue #1 tells us that one digit is a 1, but we’re not sure of its location, so we see if we can find a clue with more concrete information.
We can see that clue #5 gives us that kind of information and is the only clue that does, so we start from there.
Because this clue tells us that the thousands place digit is 2, we search for clues relevant to this clue. Clue #2 tells us that the digit in the hundreds place is three times that of the thousands place digit, so it is 6.
2 6 _ _
So now we need to find the tens and ones place digits, and see that clue #3 tells us that the digit in the ones place is four times the digit in the tens place. But we remember that clue #1 tells us that there’s a one somewhere, and since one is not four times any digit, we see that the one must be in the tens place, which leads us to the conclusion that the digit in the ones place is four. So then we conclude that our number is:
2 6 1 4
If you were following closely, you would notice that clue #4 was never used. It is a nice way to check our answer, since the digits of 2614 do indeed add up to be thirteen, but we did not need this clue to solve the problem.
Recall that the clues’ relevance were identified and prioritized as follows:
By identifying and prioritizing information, we were able to make the information given in the problem seem less overwhelming. We ordered the clues by relevance, with the most relevant clue providing us with a starting point to solve the problem. This method also utilized the more general method of breaking a problem into smaller and simpler parts to make it easier to solve.
Now let’s look at another mathematical problem and another general problem-solving method to help us solve it:
Two trees with heights of 20 m and 30 m respectively have ropes running from the top of each tree to the bottom of the other tree. The trees are 40 meters apart. We’ll assume that the ropes are pulled tight enough that we can ignore any bending or drooping. How high above the ground do the ropes intersect?
Let’s solve this problem by representing it in a visual way, in this case, a diagram:
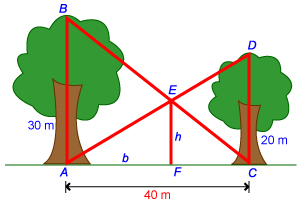
You can see that we have a much simpler problem on our hands after drawing the diagram. A, B, C, D, E, and F are vertices of the triangles in the diagram. Now also notice that:
b = the base of triangle EFA
h = the height of triangle EFA and the height above the ground at which the ropes intersect
If we had not drawn this diagram, it would have been very hard to solve this problem, since we need the triangles and their properties to solve for h. Also, this diagram allows us to see that triangle BCA is similar to triangle EFC, and triangle DCA is similar to triangle EFA. Solving for h shows that the ropes intersect twelve meters above the ground.
Students frequently complain that mathematics is too difficult for them, because it is too abstract and unapproachable. Explaining mathematical reasoning and problem solving by using a variety of methods, such as words, numbers, symbols, charts, graphs, tables, diagrams, and concrete models can help students understand the problem better by making it more concrete and approachable.
Let’s try another one.
Given a pickle jar filled with marbles, about how many marbles does the jar contain?
Problems like this one require the student to make and use estimations. In this case, an estimation is all that is required, although, in more complex problems, estimates may help the student arrive at the final answer.
How would a student do this? A good estimation can be found by counting how many marbles are on the base of the jar and multiplying that by the number of marbles that make up the height of the marbles in the jar.
Now to make sure that we understand when and how to use these methods, let’s solve a problem on our own:
How many more faces does a cube have than a square pyramid?
The answer is B. To see how many more faces a cube has than a square pyramid, it is best to draw a diagram of a square pyramid and a cube:
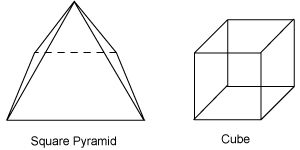
From the diagrams above, we can see that the square pyramid has five faces and the cube has six. Therefore, the cube has one more face, so the answer is B.
Before we start having the same problem our model student in the beginning did—that is, being overwhelmed with too much information—let’s have a quick review of all the problem-solving methods we’ve discussed so far:
Along with learning methods and tools for solving mathematical problems, it is important to recognize and avoid ways to make mathematical errors. This section will review some common errors.
These involve drawing a conclusion from a premise that is itself dependent on the conclusion. In other words, you are not actually proving anything. Circular reasoning often looks like deductive reasoning, but a quick examination will reveal that it’s far from it. Consider the following argument:
While this may be a simplistic example, you can see that there’s no logical procession in a circular argument.
Simply put: The fact that A implies B doesn’t not necessarily mean that B implies A. For example, “All dogs are mammals; therefore, all mammals are dogs.”
Watch out for this one. You cannot automatically assume the inverse of a given statement is true. Consider the following true statement:
If you grew up in Minnesota , you’ve seen snow.
Now, notice that the inverse of this statement is not necessarily true:
If you didn’t grow up in Minnesota , you’ve never seen snow.
This mistake (also known as inductive fallacy) can take many forms, the most common being assuming a general rule based on a specific instance: (“Bridge is a hard game; therefore, all card games are difficult.”) Be aware of more subtle forms of faulty generalizations.
It’s a mistake to assume that because two things are alike in one respect that they are necessarily alike in other ways too. Consider the faulty analogy below:
People who absolutely have to have a cup of coffee in the morning to get going are as bad as alcoholics who can’t cope without drinking.
False (or tenuous) analogies are often used in persuasive arguments.
Now that we’ve gone over some common mathematical mistakes, let’s look at some correct and effective ways to use mathematical reasoning.
Let’s look at basic logic, its operations, some fundamental laws, and the rules of logic that help us prove statements and deduce the truth. First off, there are two different styles of proofs: direct and indirect.
Whether it’s a direct or indirect proof, the engine that drives the proof is the if-then structure of a logical statement. In formal logic, you’ll see the format using the letters p and q, representing statements, as in:
If p, then q
An arrow is used to indicate that q is derived from p, like this:
p → q
This would be the general form of many types of logical statements that would be similar to: “if Joe has 5 cents, then Joe has a nickel or Joe has 5 pennies “. Basically, a proof is a flow of implications starting with the statement p and ending with the statement q. The stepping stones we use to link these statements in a logical proof on the way are called axioms or postulates, which are accepted logical tools.
A direct proof will attempt to lay out the shortest number of steps between p and q.
The goal of an indirect proof is exactly the same—it wants to show that q follows from p; however, it goes about it in a different manner. An indirect proof also goes by the names “proof by contradiction” or reductio ad absurdum. This type of proof assumes that the opposite of what you want to prove is true, and then shows that this is untenable or absurd, so, in fact, your original statement must be true.
Let’s see how this works using the isosceles triangle below. The indirect proof assumption is in bold.
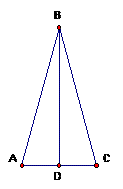
Given: Triangle ABC is isosceles with B marking the vertex
Prove: Angles A and C are congruent.
Now, let’s work through this, matching our statements with our reasons.
Some math problems work on the mechanics that statements are “always”, “sometimes” and “never” true.
Example: x < x2 for all real numbers x
We may be tempted to say that this statement is “always” true, because by choosing different values of x, like -2 and 3, we see that:
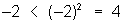
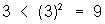
This statement will be true for all negative values of x, and most positive values of x. However, this statement is false for 0 ≤ x ≤ 1. To see this, let x =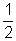 
; then we get x2 = 
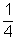. In this case, it is not true that x < x2, which means that our statement is “sometimes” true—it is true for some real numbers x.
Example: For all primes x ≥ 3, x is odd.
This statement is “always” true. The only prime that is not odd is two. If we had a prime x ≥ 3 that is not odd, it would be divisible by two, which would make x not prime.