 username@email.com
username@email.com
The following lessons will examine whole numbers, rational and irrational numbers, integers, and their attendant operations. We’ll also review prime factorizations, divisibility rules, and other basic topics pertaining to numbers.
For some of you, it’s been a long time since you’ve darkened the doorway of a math classroom. And even for those of you who have a math background, it’s helpful to review some of these key concepts from the ground up. So, let’s start at mathematics’ atomic level: numbers. Mathematicians have created a dizzying array of numbers—imaginary, surreal, and transcendental, to name just a few. Fortunately for us, we only need to learn the basics. The diagram below shows the sets of numbers that we’ll review here.
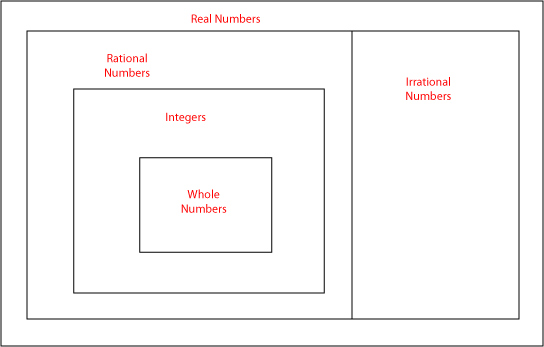
Many numbers fit into several sets of numbers. Think about putting the number into its most restrictive set in the diagram above, and then you’ll be able to see how a number can exist in more than one set.
For example, –7 is a real number, rational number, and integer, but it is not a whole number because it is negative.
What categories does √18 fit into? You should be thinking irrational number and real number.
How about √9? Since the square root of 9 is 3, it fits into the categories of real number, rational number, integer, and whole number.
Try this one on your own:
Choose the correct statement below:
The correct answer is B. The category of rational numbers is a subset of real numbers, as shown on the diagram. You can correct statements A and D by changing the first words to “some.” Correct C by making the first word “all.”
You may be thinking the whole thing doesn’t make sense at this point. Let’s take these numbers and lay them out in a traditional way.
You can do more than you might have thought you could, especially if you haven’t thought about it in a few years. Today, students of all ages use number lines for a wide variety of mathematical tasks, including:
Many students want all of their number lines to start at zero, but a number line can start and end at any number.


If the problem had been x – 3 ≥ 2, then the solution would have been x ≥ 5. On the number line, the dot on the 5 would be solid, showing that 5 is included in the solution.

Which point represents √3?
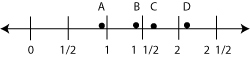
The correct answer is C. The square root of 3 is approximately 1.7, so it belongs in between 1.5 and 2.
The operations of addition and multiplication have a number of known properties that allow us to manipulate numbers and make the math easier. It can be challenging to remember all of these, so we have included some mnemonics to help you.
Commutative Property: ORDERRemember: If you live in a community it doesn’t matter where you live in it, you are still a part of the community. |
||
|---|---|---|
| Addition | Order is not important when adding numbers. | 4 + 7 = 7 + 4 |
| Multiplication | Order is not important when multiplying numbers. | 8 x 3 = 3 x 8 |
Associative Property: GROUPINGRemember: You spend time with your associates in a group. |
||
|---|---|---|
| Addition | The grouping of numbers is not important when adding numbers. | 3 + (4 + 7) = ; (3 + 4) + 7 = |
| Multiplication | The grouping of numbers is not important when multiplying numbers. | 2 x (8 x 3) = ; (2 x 8) x 3 = |
Neither the associative nor the commutative property works for subtraction or division. Grouping and order make a huge difference when subtracting and dividing!
Identity Property: SELFRemember: The number wants to stay the same; it wants to be itself. |
||
|---|---|---|
| Addition | Any number plus zero equals that number. | 4 + 0 = 4 |
| Multiplication | Any number times one equals that number. | 8 x 1 = 8 |
These properties are also called the additive identity and the multiplicative identity.
Identity Property: SELFRemember: The number wants to stay the same; it wants to be itself. |
||
|---|---|---|
| Multiplication | Any number times zero is zero. | 8 x 0 = 0 |
Time for a practice question on the associative, commutative, and identity properties.
Which number sentence below illustrates the commutative property?
The correct answer is D. Although there are three numbers, it is still the order of the numbers that has changed. This is the only answer choice in which the order of the numbers is different.
The last property that we’ll cover is the distributive property. The distributive property combines together addition (or subtraction) and multiplication. The idea behind the distributive property is that it doesn’t matter if you find the product of the sum/difference or the sum/difference of the product.
Algebraically, the distributive property is represented this way:
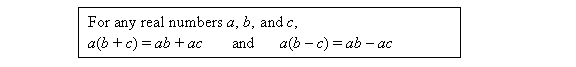
Can you multiply 9 x 47 in your head? Try it with the distributive property instead of replicating the paper-and-pencil mentally.
Did you get 423? It should have worked this way:
First thought: 9 x 40 = 360
Second thought: 9 x 7 = 63
Third thought: 360 + 63 = 423
Not too hard, we hope. Try one more.
What is 15 x 34?
Did you get 510? Think 15(30 + 4) = (15 x 30) + (15 x 4) = 450 + 60 = 510
In algebra, the distributive property is often used to expand or simplify expressions so that an equation can be solved. (Reversing the distributive property is called factoring, a topic that will be covered later in this module.)
Let’s see how this works in practice. We’ll use the distributive property to simplify the expressions below.
6(x + 2y)
Distributing the 6, we arrive at 6x + 12y.
Here is one for you to try on your own.
Which answer choice shows the expression correctly simplified?
5(3c + 5d) – 2d
The correct answer is A. First distribute the 5 to the (3c + 5d), which gives you 15c + 25d (choice B). Then subtract 2d from 25d, which leaves 23d. The answer is 15c + 23d.
This video demonstration shows how to use manipulatives to teach basic numbers skills.