⬅ Previous Lesson Workshop Index Next Lesson ➡

Proofs

Objective

In the coming lesson, we’ll explore geometric proofs related to triangles and parallel lines.

Previously Covered

In the section above, we reviewed basic three-dimensional figures and some of their properties.

A mathematical proof demonstrates that, based on one or more given facts, a statement must be true. The proof itself is a sequence of statements, each justified by a postulate or a theorem, such as the Isosceles Triangle Theorem which you will see in this lesson.On the pages that follow are sample proofs that are meant to simultaneously familiarize you with proofs and reinforce some of the concepts. Remember, the notation for similar is ∼ and the symbol for congruence is ≅.

Theorems and Postulates You’ll Need

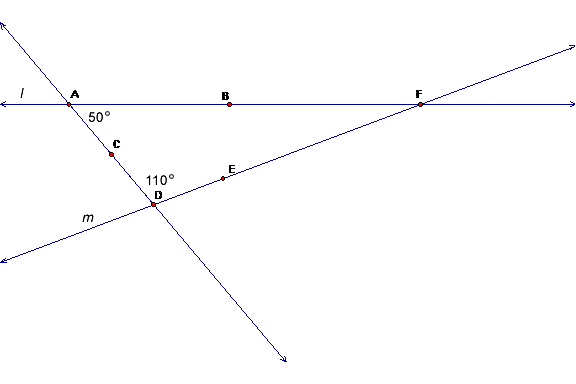
Parallel Axiom: If two lines, l and m, intersect a transversal so that the sum of the interior angles on the same side of the transversal is equal to 180°, then l and m are parallel.

If two lines, l and m, intersect a transversal so that the sum of the interior angles on the same side of the transversal is less than 180°, then l and m intersect on that side of the transversal.

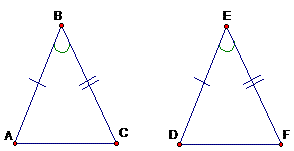
Side-Angle-Side (SAS) Triangle Congruence Theorem: If two sides and the included angle of one triangle are congruent to the corresponding sides and angle of another triangle, then the triangles are congruent.

Angle-Side-Angle (ASA) Triangle Congruence Theorem: If two angles and the included side of one triangle are congruent to the corresponding angles and side of another triangle, then the triangles are congruent.

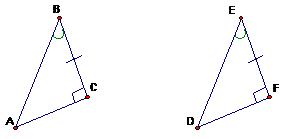
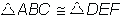
Angle-Angle (AA) Similarity Theorem: If two angles in one triangle are congruent to two angles in another triangle, then the triangles are similar. Two figures are similar if they have the same shape, but not necessarily the same size.

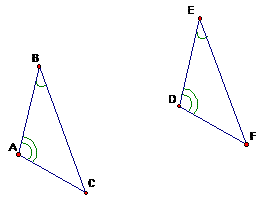
The AA theorem states that only two angles must be congruent for similarity. Do you see why this is true? Since the sums of the angles in each triangle are equal, if two angles are congruent, then the third angles must also be congruent.

Isosceles Triangle Theorem: If a triangle is isosceles, then the angles opposite the congruent sides are congruent.

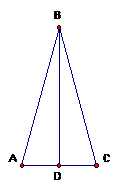
Isosceles Triangle Theorem

Let’s prove this one together. We’ll use the isosceles triangle above (△ABC) and start by bisecting ∠ABC with segment BD.

Statement	Justification
△ABC is isosceles BD is an angle bisector	Given
m∠ABD ≅ m∠CBD	Definition of Angle Bisector
AB ≅ BC	Definition of Isosceles
BD ≅ BD	Reflexive Property of Congruence
△ABC ≅ △CBD	SAS
∠BAD ≅ ∠BCD	Corresponding Parts of Congruent Triangles are Congruent (CPCTC)

Converse of the Isosceles Triangle Theorem: If two angles of a triangle are congruent, then the triangle is isosceles and the sides opposite those angles are congruent.

Converse of the Isosceles Triangle Theorem

We’ll prove this one together, as well. We’ll use △ABC above and assume that ∠BAC ≅ ∠BCA.

Statement	Justification
∠BAC ≅ ∠BCA	Given
AC ≅ AC	Reflexive Property of Congruence
∠ACB ≅ ∠CAB	Given
△ABC ≅ △CBA	ASA
AB ≅ BC	Corresponding Parts of Congruent Triangles are Congruent (CPCTC)
△ABC is isosceles	Definition of Isosceles

Basically, we proved that the triangle is congruent to itself. However, this example shows that the order that the vertices of the congruent triangles are named is important. That order tells us about the congruence of corresponding parts of the congruent triangles.

Question

Which pair of statements can be used to prove that ΔBAC ~ ΔBDE?

∠A ≅ ∠D since both angles are right angles. ∠C ≅ ∠E since vertical angles are congruent.
∠A ≅ ∠D since both angles are right angles. ∠ABC ≅ ∠DBE since vertical angles are congruent.
∠A ≅ ∠D since both angles are right angles. AC ≅ ED since both are bases of right triangles.
∠ABC ≅ ∠BDE since vertical angles are congruent. BC ≅ BE since each segment is the hypotenuse of a right triangle.

Reveal Answer

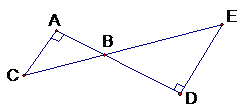
Choice B is correct. The two triangles can be shown to be similar by AA. This means that if two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. Each statement in choice B is true and shows that the pairs of angles are congruent. Choice A is incorrect, because ∠C and ∠E are not vertical angles. Choice C and Choice D contain incorrect statements.

Review

A proof demonstrates that a statement must be true. The proof itself is a sequence of statements, each justified by a postulate or a theorem.
The order that vertices are named tells us about the congruence of corresponding parts of the congruent triangles.

⬅ Previous Lesson Workshop Index Next Lesson ➡