 username@email.com
username@email.com
In this lesson, we’ll explore a few properties of polygons.
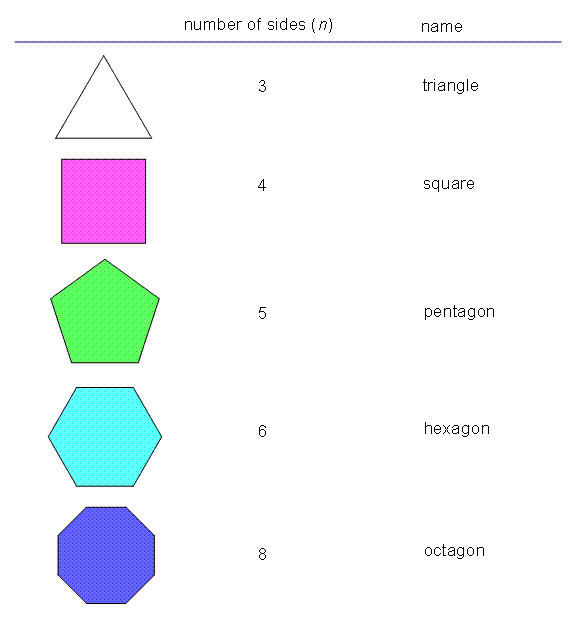
Polygons and their sides
The polygons above are the ones you’re most likely to see. The computations that you’ll do will most likely be with those above and those that are named in the table below.
| number of sides (n) | name |
|---|---|
| 7 | heptagon |
| 9 | nonagon |
| 10 | decagon |
Remember the equilateral, equiangular triangle from earlier? All of the sides and angles of that triangle are congruent. Clearly, this is a special case of a triangle, because scalene triangles do not have this property. Nor do obtuse triangles.
Which of the following figures must be equilateral and equiangular?
The correct answer is C because all of the sides and angles of a square are congruent. Choice A is incorrect, because, as perfect as they are, circles have neither sides nor angles. Choices B and D are incorrect. Both triangles and hexagons can have unequal sides and angles. For example, here’s a hexagon that is neither equilateral nor equiangular: 
A regular polygon is a polygon that is both equilateral and equiangular.
What do you call a regular quadrilateral?
Yes, it’s a square! By the way, have you found a relationship between the number of sides, angles, and vertices in a polygon? They are all equal. A triangle has three vertices, a pentagon has five sides, and a decagon has ten angles.
When you reviewed the definition of an angle earlier, you learned that an angle has an interior and an exterior. So it shouldn’t surprise you that polygons, which are composed of angles, have interiors and exteriors, as well.
An exterior angle of a polygon is the angle between one side of the polygon and the extension of an adjacent side. ∠ACB is an exterior angle of △ACD.
Assuming that △ACD is an equilateral triangle, what is the measure of ∠ACB?
The correct answer is C. Since △ACD is an equilateral triangle, it is also equiangular. Thus, each of its angles measures 60° and m∠ACD = 60°. ∠BCD is a straight angle, so it measures 180°. According to the figure, m∠ACB + m∠ACD = m∠BCD (this relationship is actually referred to as the angle addition postulate). Now substitute: 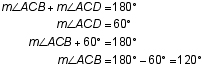
What can be learned from this one example? Well, this relationship is true for all polygons: The sum of the measures of a pair of interior and exterior angles of a polygon is 180°. That is, they are supplementary.