username@email.com
username@email.com
This next section will help you brush up on exponents and fractional exponents. This will also be a refresher on roots and scientific notation.
No, wait, that should be exponent rules. This section is filled with all the rules you need to know for dealing with numerical exponents.
First, let’s review the terminology:
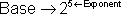
Two is the base. Five is the exponent. The whole thing (25) is called a power.
Now we’ll start with the basic rules.
| Basic Rules of Exponents | ||
|---|---|---|
| Rule | Definition | Example |
| Raising to the First Power | For any non-zero number a, a1 = a. | 61 = 6 |
| Raising to the Zero Power | For any non-zero number a, a0 = 1, by definition. | 60 = 1 |
| Negative Exponents | For any non-zero number a and integer n, a-n = 1/an. |   |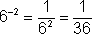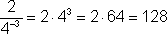
Here is one for you to practice on your own.
Write the following expression with positive exponents: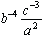 
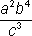
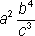
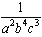
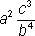
The correct answer is C. The a2 term stays in the denominator because its exponent is positive. The b-4 term must move into the denominator to make its exponent positive. The c3 term must move into the denominator to make its exponent positive, which gives you a final answer of .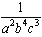
Here are the more complex rules.
| Advanced Rules | ||
|---|---|---|
| Rule | Definition | Example |
| Multiplying Powers with the Same Base | For any non-zero number a and integers m and n,  . |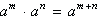
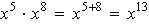
(Add the exponents when multiplying numbers with the same base.) |
| Raising a Power to a Power | For any non-zero number a and integers m and n, (am)n = amn. | (x5)2 = x10
(Multiply the exponents when a power is raised to a power.) |
| Raising a Product to a Power | or any non-zero numbers a and b, and integer n, (ab)n = an x bn. |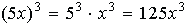 
(Each part of the product is separately raised to the power.) |
| Raising a Quotient to a Power | For any non-zero numbers a and b, and integer n, (a/b)n = an/bn | (x/5)3 = x3/53 = x3/125
(Each part of the quotient is separately raised to the power.) |
When simplifying expressions with exponents, numbers raised to a power should be multiplied out.
Simplify the expression (3d)4(d2)3
The correct answer is D. (3d)4 is equal to 34d4, or 81d4. (d2) 3 is equal to d6 because you multiply the powers when you raise a power to a power. Then add the powers when you multiply 81d4 • d6, to get 81d10
The opposite operation of raising a number to a power is to take its root. Square roots are the root with which we are most familiar. Taking the square root is essentially removing the square from the number.
62 = 36
√36 = 6
(Technically, √36 can also be (-6), since (-6)2 also equals 36.)
To find roots other than the square root, follow the same process. Without a calculator, you can really only find perfect roots. You do this by working backwards and using mental math. To find the √36, you have to think, some number times itself equals 36. Algebraically, it would look like:
x • x = 36
For a cube root, it is the same, only there are three Xs instead of two.
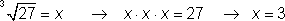
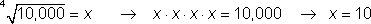
Solve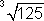 
The correct choice is A. 5 • 5 • 5 is 125. On problems like this, you can always work backwards from the answer choices.
Finding fractional powers are like finding roots. Fractional powers require a bit of logical thinking, but, for our purposes, we can examine some problems that only require some brainpower.
Briefly, here is the theory behind fractional powers. Let’s look at it with the help of an example.
161/2 = x
161/2 • 161/2 = 161/2+1/2 = 161
Utilize the rule of multiplying powers with the same base.
Now go back and replace 161/2 with x.
x • x = 161
So x = 4, which means that 161/2 = 4. That is the same as the square root of 16.
How about 491/2?
You should have said 7.
Other fractional powers with a numerator of 1 work the same way, so a power of 1/3 is just like finding the cube root of the given number.
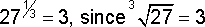
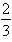power, we still find the cube root, which is 3, but we need it twice. Multiply 3 x 3 and you get 9.
323/5 = ?
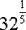= 2
2 • 2 • 2 = 23 = 8
So, 323/5 = 8
Solve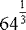 
The correct answer is B. Finding a number to the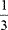 
power is the same as finding the cube root of the number, and 4 is the cube root of 64.
Exponents can seem a bit esoteric; they aren’t exactly the sort of math you need to use to balance your checkbook. But scientific notation is a fairly common use of powers and exponents.
Scientific notation is especially useful for expressing very large numbers (think astronomy) and very small numbers (think microbiology).
Numbers written in scientific notation are composed of two parts. The first part is a number between 1 and 10 (it doesn’t have to be a whole number, many are decimal numbers). There can only be one digit to the left of the decimal, so the largest number is really 9.999…. not 10. The second part is 10 raised to a power, which can be negative or positive. The two parts are multiplied together, so that they look like these examples:
3.24 x 105
9.7021 x 10-3
To write a number given in scientific notation as a number in standard form, you move the decimal point. The basic numbers of the notation do not change; the decimal moves, and you may need some placeholder zeroes.
The number of places the decimal moves is equal to the exponent.
For a positive exponent, move the decimal to the right—you are making a big number.
For a negative exponent, move the decimal to the left—you are making a small number (But remember: You are not making a negative number.) Multiplying by 10−3 is the same as dividing by 103.
3.24 x 105 = 324,000 (move the decimal 5 places to the right, filling in the 3 extra places with zeroes)
9.7021 x 10−3 = 0.0097021 (move the decimal 3 places to the left, filling in the 2 extra places with zeroes)
Now it is your turn to practice.
Write 7.059 x 108 in standard form.
The correct answer is C. Move the decimal 8 places to the right, which means you will need 5 placeholder zeroes. Put the commas in to make the number easier to read. Note that choice A has the right number of zeroes, but the decimal point is in the wrong place.
To write a number given in standard form as a number in scientific notation, there are two steps.
First, write the decimal number. Remember, you can only have one place to the left of the decimal. You can have as many places to the right as necessary. Drop any placeholder zeroes.
517,000 becomes 5.17; 0.0004906 becomes 4.906
Second, raise the 10 to the correct power. To determine the power, count how many places you needed to move the decimal to make your decimal number. The exponent will be positive if the standard form was a big number (greater than 1). The exponent is negative if the standard form of the number is between 0 and 1.
517,000 = 5.17 x 105 (the decimal has to move 5 places)
0.0004906 = 4.906 x 104 (the decimal has to move 4 places)
Write 0.00259 in scientific notation.
The correct answer is B. It has the decimal number properly formatted, and the number of the exponent is correctly counted. Choice D is similar, but the original number was positive, so the negative sign belongs to the exponent, not the decimal number.
There are a number of rules for working with exponents and powers. Most importantly: