Your Dashboard username@email.com
⬅ Previous Lesson Workshop Index Next Lesson ➡

Fundamental Theorem of Arithmetic

Objective

In this lesson, you will study and apply the Fundamental Theorem of Arithmetic and theoretic number concepts of primes, factors, and multiples.

Previously Covered:

  1. A prime number is a number divisible only by 1 and itself.
  2. A composite number is a number with factors other than 1 and itself.

What is the Fundamental Theorem of Arithmetic?

The Fundamental Theorem of Arithmetic states that every positive integer (except the number 1) can be represented in exactly one way apart from rearrangement as a product of one or more prime numbers. Basically, this means that any number (except 1) can be broken down into its prime factorization.

How do I find the prime factorization of a number?

The prime factorization of a number is made up of all the numbers’ divisors that are prime numbers.

To find the prime factorization of a number, create a factor tree.

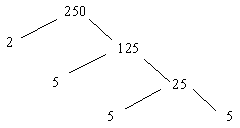
The prime factorization of 250 is 2 · 5 · 5 · 5.

Question

Which of the following shows the correct prime factorization of 120?

  1. 2 · 60
  2. 12 · 10
  3. 2 · 6 · 10
  4. 2 · 2 · 2 · 3 · 5

Reveal Answer

The correct answer is D. All answer choices are factorizations of 120, but choice D is the only prime
factorization. Each of the numbers is divisible only by 1 and itself.

What is the LCM?

The LCM stands for the least common multiple of a set of numbers. It is the smallest number that is a multiple of all numbers in a set.

How do I find the LCM?

To find the LCM, first find the prime factorization of each number in the set. Then look for the greatest number of times each factor appears in any of the factorizations. Multiply these together to find the LCM.

Find the LCM of 4, 6, and 18.

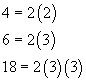
4 = 2 time 2, 6 = 2 times 3, and 18 = 2 times 3 times 3
The LCM of 4, 6, and 18 is 2 · 2 · 3 · 3 = 36, since 2 appears twice in the factorization of 4 and three appears twice in the factorization of 18.

Question

Which number is the LCM of 12, 21, and 24?

  1. 3
  2. 168
  3. 6,048
  4. 24

Reveal Answer

The correct answer is B. First, find the prime factorization of each number in the set.

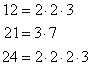
Then look for the greatest number of times each factor appears in any of the factorizations. The LCM is 2 · 2 · 2 · 3 · 7 = 168.

What is the GCF?

The GCF stands for the greatest common factor of a set of numbers. It is the largest number that is a factor of all numbers in a set.

How do I find the GCF?

To find the GCF, first find the prime factorization of each number in the set. Then look for all numbers that appear in all lists. Multiply these numbers to find the GCF. If there are no common prime factors, the GCF of the set is 1.

Find the GCF of 30, 50, and 70.

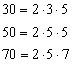
Both 2 and 5 appear in all three factorizations. Multiply them together and find that the GCF of 30, 50, and 70 is 2 · 5 = 10.

Question

What is the GCF of 18, 30, and 42?

  1. 6
  2. 18
  3. 210
  4. 630

Reveal Answer

The correct answer is A. First, find the prime factorization of each number.

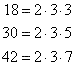
Since both 2 and 3 appear in all three factorizations, the GCF is 2 · 3 = 6.

Important Tidbit

Remember that the LCM will be no smaller than the largest number in the set. The GCF will be no bigger than the smallest number in the set.

⬅ Previous Lesson Workshop Index Next Lesson ➡

Back to Top