 username@email.com
username@email.com
In this lesson, you will solve systems of linear equations using both the reduced row-echelon method and the Gauss-Jordan elimination method.
Reduced row-echelon form of a matrix is the form of a matrix in which:
There are a number of moves that can change a matrix into reduced row-echelon form. But before we learn these moves, we will first examine the connections between matrices and linear equations.
For example, a school band decides to purchase xylophones and zithers. If xylophones cost $30.00, and zithers cost $40.00, how many of each should they buy in order to purchase exactly 254 instruments and spend their entire budget of $8,500?
Two Perspectives on the Solution
Let x = the number of xylophones.
Let z = the number of zithers.
x + z = 254
30x + 40z = 8,500
Standard Elimination Method
Matrix Method
x + z = 254
30x + 40z = 8,500
![]()
The above equation can also be represented
![]() .
.
In order to solve the system using matrices, we use moves (called row operations) similar to those on the left. The following row operations are acceptable:
These row operations may be used in combination.
The amount of writing is reduced by committing the variables to memory, removing the variables from the matrix, and writing the matrix equation in augmented form as shown below.
![]()
The row operations used to maneuver the matrix into reduced echelon form are described below.
–30x – 30z = –7,620
30x + 40z = 8,500
10z = 880
![]()
z
= 88
![]()
This augmented matrix represents
![]() ,
,
meaning x + z = 254,
Use row operations and:
When all rows are completed, use back-substitution to determine the value of each variable.
Reduced row-echelon form works well, but the Gauss-Jordan method is better for those who do not like to do back-substitution.
The Gauss-Jordan elimination method is similar to the reduced row-echelon method, but avoids back-substitution by continuing the row operations until the left side of the matrix has a diagonal (in a negative slope) with entries of 1 and all other entries of 0. The entries on the right side of the matrix may or may not be 0.
The matrix below has been subjected to the Gauss-Jordan elimination method. Notice how easy it is to read the solution to this system of four equations.

The first variable is equal to –2.
The second variable is equal to 0.
The third variable is equal to 6.
The fourth variable is equal to
![]() .
.
The approach is to start in the reduced row-echelon method form, but instead of back-substitution, continue row operations. The idea is to first focus on the column above the last initial entry of 1. When all the entries in that row are 0, then do the same on the column to the left. Continue moving to the left until the final form is achieved.
Let’s look at the former example.
![]()
For us to convert this matrix to the Gauss-Jordan elimination final form, the only thing we need to do is make the second entry in row 1 into a 0. We can achieve this by multiplying row 2 by –1 and adding it to row 1, thus replacing row 1.
![]()
This matrix can also be viewed as
![]() .
.
Notice how easy it is to identify the solutions x = 166 and z = 88.
Solve the following system of equations using the Gauss-Jordan elimination method.
2a + b + c = 5
2a + b – 3c = 9
3a + 2b + 5c = 2
The matrix equation is
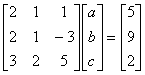 .
.
The augmented matrix is
 .
.
(Row 3 – row 1 becomes row 1.)
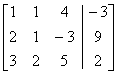
(–2 times row 1 + row 2 becomes row 2.)
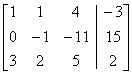
(–3 times row 1 + row 3 becomes row 3.)
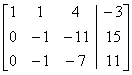
After the first row is complete, the second entry
in row 2 needs to become 1.
(–1 times row 2 becomes row 2.)

(Row 2 + row 3 becomes row 3.)
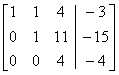
(Multiply row 3 by 0.25.)
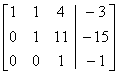
(–11 times row 3 + row 2 becomes row 2.)
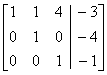
(–4 times row 3 + row 1 becomes row 1.)

(Row 1 – row 2 becomes row 1.)
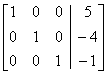
a = 5
b = –4
c = –1