 username@email.com
username@email.com
In this lesson, you will use proportions to compute arc lengths and areas of sectors of circles. You will also apply proportions to interpret scale drawings and maps.
A sector is a portion of a circle. The area of a sector can be found by setting up a proportion using the angle measure of the sector, the central angle of the circle, and the area of the entire circle.
Let’s try an example. Find the area of a sector with an angle of 20˚ in a circle with radius 15 meters.
The entire area of the circle would be ![]() square meters.
square meters.
The area of the sector is proportionate to the ratio of the angle of the sector over the central angle of the circle.
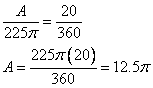
Thus, the area of the sector would equal ![]() square meters.
square meters.
Finding an arc length is similar to finding the area of a sector. The arc length is a part of the circumference of a circle, so its length is proportionate in a way similar to the way a sector’s area is proportionate to its angle.
Find the arc length of the sector of the circle described in the previous example.
The circle has a circumference of ![]() .
.
The arc length can be found using a proportion.
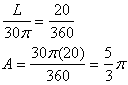
What is the area of a sector of a circle with radius 12 centimeters, with measure between radii ![]() radians?
radians?
The correct choice is B. The ratio of the areas is equal to the ratio of the angles.
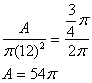
What is the arc length of a ![]() -radian sector of a circle with radius 12 centimeters?
-radian sector of a circle with radius 12 centimeters?
The correct choice is A. The ratio of the arc lengths is equal to the ratio of the angles.
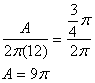
Maps of states or drawings of buildings are not drawn life sized because it would never fit on the paper. Instead a scale drawing is made. The scale is usually identified on the map or drawing.
Let’s try an example. Find the length of the actual car if a ![]() scale model is 12 inches long.
scale model is 12 inches long.
The ratio of the length of the model to the actual car is ![]() .
.
![]()
The Washington Monument is 555 feet tall. If a scale model is made that is 30 inches tall, which of the following represents the scale of the model?
The correct choice is D. Convert 555 ft to inches: (555)(12)=6,660 in. The scale of the model is 30 in/6,660 in = 1/222.