username@email.com
username@email.com
In this lesson, we will define and thoroughly investigate the Pythagorean trigonometric identity.
in right triangles (where side c is the hypotenuse, and sides a and b are legs). Trigonometric identities are equations that are always true and can simplify complex functions.
What is a Pythagorean trigonometric identity?
The trigonometric identity involving cosine and sine is 
. This identity is known as the Pythagorean trigonometric identity because it can be derived using the Pythagorean Theorem, and, in turn, the Pythagorean Theorem can be derived using the Pythagorean trigonometric identity. There are two other identities, referred to as Pythagorean identities, that can be derived using this identity.
You should be able to derive the Pythagorean trigonometric identity using the Pythagorean Theorem.
Using the trigonometric ratios and the triangle below, we can say that
Divide both sides by the hypotenuse squared.
1 =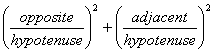 
Since 
, and 
, we can use substitution and get
If you begin by assuming that the Pythagorean trigonometric identity is true, can you work backwards and end up with the Pythagorean Theorem?
Now, we will hit the brakes and try to do what we did above, but in reverse. We will try to end up with the Pythagorean Theorem, beginning with the identity 
. This process may be a bit too complicated to attempt on your own, so we will go through this one together.
Start by using the identity
.
On the unit circle below the x– and y-axes, we can see 
and 
, on the right triangle inside of the unit circle. The easiest way to continue is to pull the right triangle out of the circle for evaluation purposes.
If we use substitution, we get
.
And using the basic trigonometric ratios, we know that 
, and 
.
So we can use substitution again to get
.
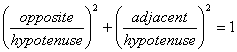
Now multiply both sides by 
.
And since the side opposite of 
is a, the side adjacent to 
is b, and the hypotenuse is c, we get
.
And since 
is the Pythagorean Theorem, we have derived the Pythagorean Theorem from the trigonometric identity 
.
The other two trigonometric identities that can proved using the Pythagorean trigonometric identity that involves sine and cosine are 
and 
.
Try and prove that 
, using the Pythagorean trigonometric identity that involves sine
and cosine.
Now divide both sides by 
and you get:
.
In the previous section, you learned that 
, and that 
. So, using substitution, you find that:
.
Try to derive the trigonometric identity 
, beginning with the Pythagorean trigonometric identity that involves sine and cosine.
Divide both sides by 
.
Since we learned in the previous section that 
, and that 
, we can use substitution to get:
.
These three trigonometric identities need to be memorized. But if you can derive two of the three from the Pythagorean trigonometric identity involving sine and cosine, then there are two less formulas you will need to remember. This is why it is a good idea to know how to derive formulas and identities. If you forget an identity, you can always derive it from another one you know!
These are the three most well known identities, but there are many more, some of which will be discussed in a later section.
How do you use these trigonometric identities?
As we discussed earlier, a trigonometric identity is an equation that is always true and can simplify a complex equation. The best way of learning how to use these identities is to practice, practice, practice.
What is the correct simplification of the expression 
?
The correct choice is C.
Since we know that 
, and 
, we can use substitution.
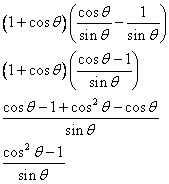
Using the Pythagorean trigonometric identity 
, we know that 
. If we use substitution, we find that
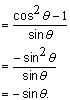
You can look at using these trigonometric identities as a game. The better you are at using these, the easier trigonometry is going to be. So try making up your own expressions, and try simplifying them using Pythagorean trigonometric identities.
