username@email.com
username@email.com
In this lesson, we will define rectangular and polar coordinates and discuss the differences between and how to convert between these two different types of coordinates.
Rectangular coordinates are coordinates stated in the form (x, y). You are probably already familiar with rectangular coordinates from previous experiences. You may have used rectangular coordinates in the past without realizing what they were called. the point (3, 3), given in rectangular coordinates, is graphed below.
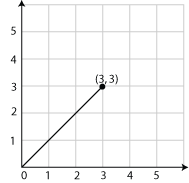
As you can see, this point is 3 units to the right of the origin along the x-axis, and 3 units up from the origin along the y-axis.
Polar coordinates are stated in the form (r, 
), where r is the distance from the origin to the point, and 
is the angle between the positive x-axis and the ray from the origin to the point. An example of the polar coordinates (r, 
) is shown below.
Pay close attention to which form is being used!
In both forms, an ordered pair denotes a point. It is impossible to determine which system is being used if you are simply given an ordered pair, but not told which type of coordinate it is. You may think that a point given as (2, π) must be in polar coordinates, since it contains what appears to be a radian measure of an angle, but (2, π) is also a perfectly valid point in the rectangular coordinate system. A well stated problem will always let you know which system is being used.
You can convert from polar to rectangular coordinates using the trigonometric ratios that you learned earlier and the diagram of polar coordinates shown below.
A right triangle can be inserted into the diagram. This step may look familiar because it is very similar to the process we used in the section on the unit circle.
The legs of the right triangle are designated x and y because they represent the x- and y- axes. We want x and y to be stated in terms of polar coordinates (r, 
). Using the trigonometric ratios, we know that
.When solving for y, you get 
.
We also know that 
. When solving for x, you get 
.
From this process, we can conclude that the equation for converting polar coordinates to rectangular coordinates is:
Which choice correctly converts polar coordinates 
to rectangular coordinates?
)
)
)
)The correct choice is A. We know r = 4 and 
and 
, so using substitution, you get
,
and
.
So converting polar coordinates 
into rectangular coordinates equals 
.
Using the diagram of the rectangular coordinates (x, y) above, you can see that a right triangle can be inserted in this graph also.
Again, we have legs x and y, and since we are trying to convert from rectangular coordinates to polar coordinates, we need to solve for r and 
in terms of x and y.
We know by the Pythagorean Theorem, that 
.
Take the square root of both sides to get 
.
Now that we have solved for r in terms of x and y, we need to solve for 
in terms of x and y.
By the trigonometric ratio, we know that
Solving for 
by using our inverse trigonometric rule, we know that
From this process, we can conclude that the equation that converts rectangular coordinates to polar coordinates is:
.
Which choice shows rectangular coordinates (2, 2) converted to polar coordinates?
The correct choice is C. We know that x = 2 , y = 2, and . So using substitution you get
,
and
.
So, converting rectangular coordinates 
into polar coordinates equals 
.
Not only can you convert between polar and rectangular coordinates, but you can also convert a polar equation into a rectangular equation or vice versa by using substitution.
Which choice shows the equation y = 3x + 2 in polar form?
The correct choice is C.
Since we know 
and 
, we can use substitution to get
.
How do you write complex numbers in polar form?
Complex numbers are numbers which contain both a real part and an imaginary part. Remember, imaginary numbers and complex numbers are not the same thing. Imaginary numbers are scalar multiples of i, where i = 
. Some examples of imaginary numbers are 5i, –6.2i, and –i. Complex numbers have two parts, a real part and an imaginary part, and are written as the sum of these two parts. Some examples of complex numbers are 3 + 5i and 298 – 9.3i. We traditionally use x and y as variables representing real numbers. For complex numbers, the letter z is commonly used. Below are plots that include complex numbers. A complex number can be thought of as z = x + yi, where x is the real part of z and yi is the imaginary part. To graph a single real number, we need only one axis. To graph a single complex number, we need two axes—one to keep track of the real part of our number, and one to keep track of the complex part. We measure the real part of the number along the x-axis, and the imaginary part along the y-axis. The graph below on the right illustrates how the complex number z = 3 + 3i can be graphed in this way. The same complex number can be denoted using polar coordinates as well. The graph on the left illustrates how we can begin thinking about writing complex numbers in this form.
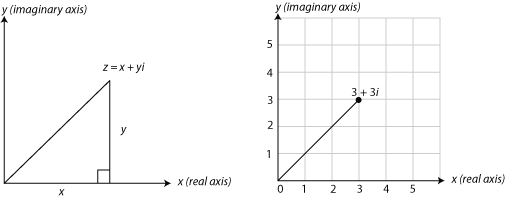
Take a minute and use the information from this lesson to determine how to write complex number in polar form.
You know that 
.
So, you have 
. Using substitution, you get
This is the formula for complex numbers in the polar form.
What is the polar form of the complex number z = 5 – 5i?
, 
)
(cos 
+ i sin 
)
)
+ i sin 
)The correct choice is B.
z = 5 – 5i
This point will be in the 4th quadrant of the complex plane, and since the x-coordinate and y-coordinate
are both equidistant from the origin, the angle must be 
. We also know that r = 
, so r = 
. So the polar form of the complex number is therefore z = 
(cos 
+ i sin 
).
This method can be used to multiply complex numbers in the polar form. Just remember to use substitution when doing this. Try the example below.
What is y = (3i + 2)(6i – 2) in polar form?
The correct choice is D.
y = (3i + 2)(6i – 2)
Multiplying out this expression you get
.
The –18 comes from 3i being multiplied by 6i, because 
.
We know that 
and 
. So using substitution we get
An important theorem that involves complex numbers is DeMoivre’s Theorem. DeMoivre’s Theorem states that if 
, then 
. Try and prove this theorem yourself. The easiest way of doing this is to establish a pattern by starting with 
, then add a power each time you simplify the equation, until you feel comfortable with the theorem. DeMoivre’s Theorem is useful when trying to find the powers of complex numbers and to simplify complex numbers.
DeMoivre’s Theorem can also relate to addition and double angle formulas. To practice working this type of problem, try the example below.
If , where r = 4, and 
= 60°, what is 
?
The correct choice is D. By DeMoivre’s Theorem, we know that 
. And since 
, and 
= 60°, we can use substitution to get
.
Using the double angle formula 
, we know that 
= 
. And using the double angle formula 
, we find that 
. So using substitution, we get
.
), where r is the distance from the origin to the point, and 
is the angle between the positive x-axis ray from the origin to the point. 
.
, and can be useful when trying to find the powers of complex numbers, and when simplifying complex numbers.Geometry and Trigonometry for Calculus. (Peter H. Selby): John Wiley and Sons, 1976.
Precalculus. (Ron Larson): Houghton Mifflin, 2003.
Trigonometry. (I.M. Gelfand and M. Saul): Springer Verlag, 2001.
Trigonometry Demystified. (Stan Gibilisco): McGraw-Hill, 2003.
Don’t forget to test your knowledge with the Trigonometry Chapter Quiz;