username@email.com
username@email.com
In this lesson, you will study the definition and uses of relations and functions, including how to use tables, graphs, verbal rules, and symbolic rules.
In mathematics, a relation may be:
The domain of a relation is the set of all possible values for the first element in the mapping, first coordinate of the ordered pair, or x-variable in an equation or inequality. The range of a relation is all the possible values of the second element, coordinate, or y-variable.
What is the difference between a relation and a function?
A function is a relation in which each element in the domain corresponds to one, and only one, element in the range. Graphically, a curve expresses a function if any vertical line passing through the curve intersects the curve once only.
Relations and functions can be represented by tables, graphs, rules, or equations.
For example, the following table represents a relation because it is a set of ordered pairs. The domain is {1, 2, 3, 4}. The range is {2, 3, 4, 5}. The table also represents a function because each x-value has one and only one y-value.
| x | y |
|---|---|
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 5 |
Consider the set of ordered pairs {(6, 7) (8, 9) (10, 11) (12, 13)}. This set of ordered pairs is best described as being
The correct answer is C. The set is a relation because it is a set of ordered pairs. The domain is {6, 8, 10, 12}. The range is {7, 9, 11, 13}. The set is a function because each element in the domain corresponds to one element in the range. These ordered pairs can be derived from the equation 
. Thus, we know that that equation is a function.
A function can be graphed in the following way.
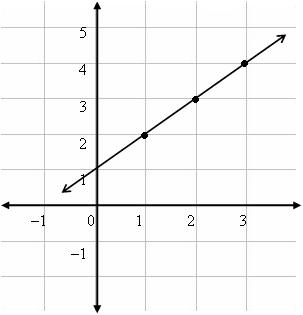
Consider the graph below.
The correct answer is C. First, we know it is a relation because each point on the curve is an ordered pair. It is a function because we cannot draw a vertical line that intersects the curve more than once.
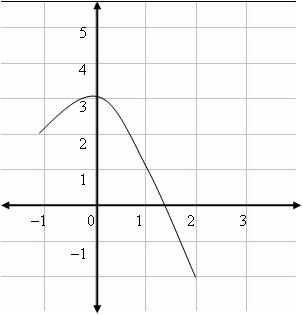
Consider the graph below.
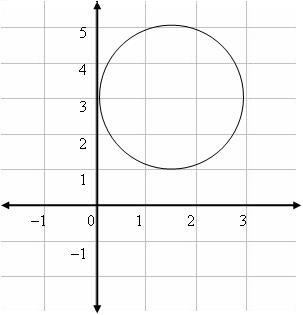
The correct answer is A. The graph depicts a relation, because the circle is made up of points representing ordered pairs. The curve is not a function, however, because you can draw vertical lines through it that intersect it more than once.
When writing a rule or an equation that represents a function, we use functional notation. That means that we replace y in the equation with ƒ(x). We can also use g(x) or h(x), or any letter through m.
So, 
becomes 
in functional notation.
To show that ordered pairs are a function, use ƒ, g, or h alone.
If 
, which choice ordered pair can be found for 
?
The correct answer is A. To find the ordered pair, substitute –2 for x and solve for f(x).
To find out, check whether any value of x produces more than one value for ƒ(x). Find out by testing various values, both positive and negative, for x. In this case, no x value can produce more than one value for ƒ(x), so the relation is a function. Note, however, that there will be two values for x, a positive one and a negative one, that map to any value of ƒ(x).
A linear function is a function that can be written in the form 
, where m and b are real numbers and m ≠ 0. For a function in this form, y, or ƒ(x) is a dependent variable, and x is an independent variable.
The simplest form of a function is called a parent function. For linear functions, 
is the parent function.
is the parent function for quadratic functions.
is the parent function of exponential functions.