⬅ Previous Lesson Workshop Index Next Lesson ➡

Utilizing Combinations and Permutations

Objective

In this lesson, you will study how to use combinations and permutations to compute probability and
learn useful simplifications created by using addition, multiplication, and complementation of known
probabilities.

Previously Covered:

The probability of a favorable outcome from an event is a number between 0 and 1, which measures the likelihood that the favorable outcome will occur by using the formula:
for the special cases where each outcome is equally likely.
The sample space of an event is the set consisting of all possible outcomes from the event.
The fundamental counting principle states that the total number of possible outcomes from a series of events is determined by multiplying all the ways that each individual event can occur.
The permutation operation is used to count the elements of the sample space when ordering r elements out of a set of n elements and when order does matter.
The combination operation is used to count the elements of the sample space when grouping r elements out of a set of n elements and when order does not matter.

How do permutations and combinations fit into determining probability?

After defining probability, we took a little detour to talk about permutations and combinations, which are really just advanced counting techniques. We did this because probability is simply a ratio of two numbers (favorable outcomes and total outcomes) and we will need to use these two techniques to make a quick and accurate count of these outcomes.

Question

Suppose you have 10 different t-shirts, one of which is your favorite. If you close your eyes and line up the t-shirts you will wear for each day next week, what is the probability you will get to wear your favorite t-shirt on Monday?

Reveal Answer

The correct choice is D. In this example, the outcome E = “I will pick my favorite t-shirt for Monday.” Notice that because we are arranging the t-shirts in a specific order, we should use permutations.

First, calculate the total number of possible ways that your t-shirts for next week can be ordered. We use to calculate the total number of ways to order 7 t-shirts out of 10.

Now we will use the fundamental counting principle to count the number of favorable outcomes for this event. List the days of the week.

For a favorable outcome, you must choose your favorite t-shirt for Monday. Thus there is only one favorable choice for Monday.

With one t-shirt spoken for, we have 9 options for Sunday’s t-shirt.

Then there are 8 options remaining for Tuesday’s t-shirt.

This leaves 7 options for Wednesday’s t-shirt, and so on.

Ultimately, we get
.

Important Tidbit

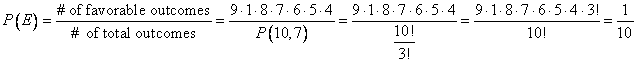We could rethink this question in the following way to justify the answer:

What if today is Monday and we want to know the probability of picking our favorite t-shirt today? Probabilistically speaking, these two situations are the same. There is only one favorable outcome out of 10 possible outcomes. This gives us .

Question

In the card game 5-card stud, each player is dealt five cards per hand. Suppose you are playing a game of 5-card stud with 4 friends. After playing the first round, the cards are thoroughly shuffled and dealt again. What is the probability that you will be dealt the exact hand you started with in the first round? (There are 52 cards in a deck.)

Reveal Answer

The correct answer is B. Since it doesn’t matter what order you are dealt the cards in your hand, you should immediately think of combinations. The cards are being dealt to you, so the dealer is choosing 5 cards out of a deck of 52. You want to get the exact hand you had in the first round, so there is only 1 favorable outcome. Therefore, .

Important Tidbit

Use combinations here because the order in which you receive the cards does not change the hand you are dealt.

How can probabilities involving two events be simplified?

Suppose there are two events, each with their own favorable outcomes , and each with their own probabilities . We can ask what is the probability of both favorable outcomes occurring, i.e., , or we can ask what is the probability of at least one of the favorable outcomes occurring, i.e.,. We can even ask what the probability is of a favorable outcome not occurring, i.e., . In all of these situations, there are simple formulas defined in terms of the known probabilities.

Important Tidbit

All probabilities are less than or equal to one, so the product of any two is never larger than either of the two probabilities considered individually. Because many probabilities are less than one and we are evaluating the likelihood of both favorable outcomes occurring, we would often expect the final probability to be smaller than the individual probabilities.

Adding two probabilities, on the other hand, increases the total probability. Because we are evaluating the likelihood of either favorable outcome occurring, we would expect the final likelihood to be greater.

Question

Suppose we pick a card at random from a deck of 52 cards while rolling a fair six-sided die. What is the probability of getting a red face card from the deck and a number less than 5 on the die? Remember that there are 12 face cards in a deck, 3 in each suit.

Reveal Answer

The correct choice is D. Here = “choosing a red face card” and = “die lands on a number less than 5.” Because you are looking for the probability of two independent events, use to make your calculations.

and

⬅ Previous Lesson Workshop Index Next Lesson ➡