username@email.com
username@email.com
In the coming sections, we’ll review the ideas of population, samples, and bias, as they pertain to data. We’ll also cover simple and compound events, and see how probability works in some different examples.
In this section, we’ll look briefly at inferences that can be made from available data, assumptions that can be made about the data, and potential sources of bias that may be inherent to the data. To do this, we need to begin with some definitions.
A population consists of an entire set of people, places, things, etc. with something in common, like all the men in my statistics class, all the women on the planet, single parents, adopted children, and jazz music. The whole point of inferential statistics is to help us infer characteristics of a population.
A sample is a subset of a population. Samples are useful when we want to draw conclusions about a population, but it is impractical to collect information from the entire population. Perhaps it’s too costly to do so or too time consuming, or maybe there are members of the population who are difficult to access for any number of reasons. Ideally, the sample has everything in common with the population. Samples like those are hard to create
But there are some ways to create samples that are more reliable than others. A random sample is a subset of a population in which every member of that population has the same chance of being chosen for the sample.
How meaningful is it to you that four out of five dentists recommend using Supercalifragi-fluoride toothpaste?
Are you suspicious? Why should you be? Maybe the sample included 1,000 doctors who were asked if they would recommend the toothpaste. Maybe there were only five doctors in the sample. Would you be more likely to buy the toothpaste if 95% of dentists surveyed use Supercalifragi-fluoride toothpaste in their own homes?
Here’s the point: Random sampling is a great way to prevent bias. Nothing about the toothpaste statements suggests any details of the study. For that reason, it’s reasonable to be suspicious.
Suppose you wanted to do a research project on liberal arts students’ attitudes toward statistics, you’re likely to get a biased sample if you advertise the study in the school paper. Do you know why?
Now suppose you’re doing a research project on the length of time students in all of the sections of a particular statistics course spend studying for the next statistics test. You assign each student a number and use a random number generator (like a computer program, for example). You get your random sample, and it contains only women. Is your sample biased? Click here to find out.
In which of the following is random sampling most likely used?
Choice A is the correct answer. A lottery uses random sampling. Typically, the winning numbers are drawn at random from all of the available numbers. Each of the available numbers has an equal chance of being picked. Choice B is incorrect: A census does not use random sampling, because every member of the population is included. Choice C is incorrect: A national election cannot use random sampling, because voting is restricted to only those who are eighteen years of age or older. Choice D is incorrect: An internet survey does not use random sampling, because members of the sample participate voluntarily.
In this section, we’ll explore basic notions of probability of simple and compound events. This exploration will rely somewhat on counting methods in order to determine sample sizes and the size of outcomes of experiments.
An event is just an experiment. Rolling a six-sided die, picking a card, and flipping a coin are all events.
The outcome of an event is the result of the experiment. There are six possible outcomes for rolling a die. There are fifty-two possible outcomes when picking one card from a standard deck of fifty-two cards. And there are two possible outcomes for flipping a coin.
The probability of an outcome in an experiment is a number, expressed as a ratio, fraction, decimal, or percent that describes the likelihood that the outcome will occur.
So, you can see that the probability of an outcome is a number between zero and one. Remember, zero = 0%, so if an outcome has a probability of zero, then there is no chance that the outcome will occur. And one = 100%, so if an outcome has a probability of one, then there is a 100% chance that the outcome will occur. Probabilities closer to zero are less likely, and probabilities closer to one are more likely.
When one die is rolled, what is the probability that the outcome is even?
Choice C is the correct answer. Of the numbers 1 through 6, three are even. So the probability of rolling an even number is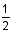 
, or 50%.
A sample space is the set of possible outcomes for an event. For example, the sample space for flipping a coin is {heads, tails}. The sample space for rolling a six-sided die is {1, 2, 3, 4, 5, 6}.
Because probability is the ratio of the number of desired outcomes to the total number of outcomes, when sample spaces get very large, techniques for counting the number of elements in a sample space are extremely useful.
For example, how many ways are there to line up ten people in a row? Actually, there are more than three million ways to do it. We definitely need an organized and systematic way to figure this out. Enter the world of permutations and probability.
In more everyday terms, a combination is an un-ordered selection from a group of objects. For example, let’s say you have fifty-two cards and select five random cards – for a hand of poker. It does not matter in what order the cards are drawn, because you can rearrange them without a loss of information. This is the crucial difference between combinations and permutations.
In more formal mathematical terms, a combination is a subset of a set. In a set of objects, the order of the objects does not matter. And since order does not matter, we are only interested in what objects are present, not their order. So, in a combination {2, 4, 6} = {6, 4, 2} = {4, 2, 6}.
On the other hand a permutation is a specifically ordered selection made from a group of objects. Lets use the card example again. This time, however, the most important aspect of our subset is its order or arrangement of objects. For example, if we drew a 5 of clubs, a J of diamonds, a 7 of spades, an 8 of clubs, and a 10 of clubs – this is NOT the same as that assemblage in a different order: a J of diamonds, an 8 of clubs, a 5 of clubs, a 7 of spades, and a 10 of clubs.
Here is an example with a set of three objects. There are six permutations of a red (R), a green (G), and a blue (B) marble:
RGB, RBG, GBR, GRB, BRG, BGR
Notice that the order matters. Every arrangement consists of all three marbles, but each gives the marbles in a different order.
As the number of items increases, the number of permutations of those items increases incredibly faster. Hence, when you hear that there are more than 5,000 ways to prepare a burger, know that it takes only seven toppings to do that.
Suppose these are the burger toppings we’ve been talking about:
{ketchup, mustard, mayonnaise, lettuce, onion, pickles, tomatoes}
Once you’ve picked one of the seven toppings and put it on your burger, there are six left to choose from. Once you’ve picked one of the six remaining toppings, there are five left to choose from – and so on. There are 5,040 ways to prepare a burger with seven toppings.
What we’ve been discussing are factorials, which are the product of all integers less than or equal to n, the number of objects in the set. This is expressed as n! For example, here’s what it looks like for a set of 4:
4! = (4)(3)(2)(1) = 24
Give it a try other examples like 5! or 10! Notice how quickly permutations get enormous. The ability to capture this information with an exclamation mark after a number is what makes mathematics such a useful symbolic language and powerful tool as we explore and learn about our world.
There are five people on a bicycle racing team. They always ride in a pace line, with one cyclist behind another. How many ways are there for the team to ride in a line?
Choice D is the correct answer. The fundamental counting principle applies here, so there are 120 ways for the cyclists to ride in a line.
A simple event consists of one trial of an experiment, like rolling a die once.
A compound event consists of more than one trial, like picking a card from a standard deck, returning it, and picking another card.
Suppose there are four coins in your pocket: a quarter, a dime, a nickel, and a penny. Suppose you pick one coin and then pick a second coin. What’s the probability that the second coin is the penny? It depends.
Two events are independent if the outcome of the first does not affect the outcome of the second. Two events are dependent if the outcome of the first does affect the outcome of the second.
Which of the following experiments is an example of two dependent events?
Choice B is the correct answer. Once Ann picks a ball from the table, there are fewer balls for Li to choose from.