username@email.com
username@email.com
Now that we have learned all of these mathematical reasoning and problem-solving techniques, we can hopefully fulfill our goal of being able to teach these techniques to students. So let’s go over some strategies and tips for successful mathematical instruction.
Example: Consider the situation where a teacher wants a student to learn how to multiply two fractions. How would this teacher systematically sequence instruction in order to achieve this goal?
Assuming that a student is already familiar with basic mathematical operations (addition, subtraction, multiplication and division), the teacher would want to teach the students about fractions:
A fraction is a rational number 
, where a is a real number called the numerator, and b is a real number not equal to zero called the denominator.
Then the teacher would want to define the product of two fractions and 
:
()() = (
)
where the numerator of the product of the two fractions is equal to the product of the numerators of the two fractions, and the denominator of the product of the two fractions is equal to the product of the denominators of the two fractions.
To end the sequence of instruction, the teacher would want to go over an example illustrating the concept of multiplying two fractions:
For any given group of students, it is most likely the case that they are coming from very different backgrounds—some of these differences being levels of knowledge, aptitude, and interest in the subject being taught.
Therefore, it is important to structure lessons in order to accommodate all of these students. How would a teacher do this? Here is a possible course of action:
Of course, you probably won’t be able to teach all of these groups individually—most teachers do not have the time or resources. One solution to this problem would be to give the entire class a lesson, and then assign each small group different problems to solve depending on their skill level. Ideally, the students would work on these problems together and help each other.
Example: If a teacher was giving a lesson on how to compute the area of simple geometric shapes, like squares and triangles, here are two different problems the teacher could give—one for a less-advanced group and one for more-advanced group.
Problem One (for the less-advanced group):
What is the area of the triangle with a height of five inches and a base three inches?
Now, what is the area of the square with one side six inches long?
Problem Two (for the more advanced group):
What is the area of the drawing of the house below, with height nine inches and base five inches wide?
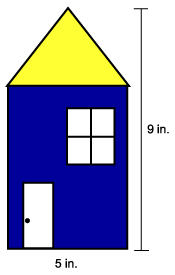
Why would the less-advanced group be assigned problem one? Because that problem simply requires computing the area of a triangle and then the area of a square. However, problem two requires a student to divide the house into a square and a triangle, compute the area of each, and then add these areas together to find the total area of the house. Thus, because problem two addresses more concepts and is not as straightforward as problem one, it would be appropriate for the more advanced group.
Example: When students have to learn how to add multiple-digit numbers, they commonly start with the left column. For example, when adding the two numbers 86 and 57, a student might start by adding the 8 and 5 to get 13.
How might a teacher correct the student’s error?
One method is to come up with a creative way for the student to remember the correct way to add two numbers. In order to add two numbers, the student needs to start by adding the numbers in the right column, so the teacher could say “starting with the left column is wrong, and starting with the right column is right! Remember: right is right!”
That way, the student would only have to remember the phrase “right is right!” when trying to add numbers with multiple digits, and thus be more likely to start by adding the numbers in the “right” column, which is the “right” way to do it.
Point out some of the practical uses of new math skills and knowledge by linking them to other subject matter, to careers, and to personal situations. This makes math more important and students will want to learn more when you can show them the power of mathematics and logic in their everyday lives.
Not only is it important for a teacher to be able to successfully teach mathematics to his/her students, but it is also important for a teacher to encourage students to be interested in mathematics and realize its importance and usefulness.