username@email.com
username@email.com
In this lesson, you will study how to identify symmetry in two- and three-dimensional objects.
Recall that a transformation of a space is an operation performed on the set of points in the space. We call the transformed point the image, while the original point is called the preimage. A two-dimensional isometry is a nontrivial rigid motion of the plane or, in other words, a transformation of the plane that preserves angles between lines and distance between points or maintains congruency.
Symmetry is a simple, fundamental geometric principle that allows us to distinguish objects. The idea of symmetry is based on isometries of space.
A plane figure has symmetry if an isometry exists mapping the object onto itself. The simplest two-dimensional symmetries are reflectional symmetry, point symmetry, and rotational symmetry.
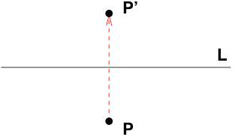
A reflection of a point P about a line L is the operation of exchanging all points of an object with their mirror images across a line L. The line L is referred to as the axis of symmetry.
A plane figure C has reflectional or line symmetry if there is a line L such that C contains the reflection across L of each point of C. The line L is called the axis of symmetry.
For example, the figure below has reflectional symmetry. The red line represents the axis of symmetry.
The reflection of a point P across a point Q is the point P’ such that Q is the midpoint of the segment PP‘. We say that the points P and P‘ are symmetric about Q.
A plane figure C is point symmetric about Q if for each point P of the figure C, C contains the reflection of P across Q. The point Q is called the center of symmetry of C.
Which of the following letters is point symmetric?
The correct answer is D.
The center of symmetry is shown in red.
A rotation is the result of turning of a plane about a fixed point by an angle. In general, we deal with rotations of angle 
, where n is a positive integer. This angle is called the angle of rotation.
A plane figure C has rotational symmetry if there is a rotation of the plane about a fixed point Q, such that for each point P of C, C contains the image of P under the rotation. Q is called the fixed point of the rotation.
The figure below is an example of rotational symmetry. What is the angle of rotation?
The correct answer is B. The star has rotational symmetry about the fixed point shown below. The star is five-pointed and, therefore, has an angle of rotation of 
.
Point symmetry is actually a special case of
rotational symmetry with a rotation angle of 180°.
Which of the two-dimensional figures below has rotational symmetry, point symmetry, and reflectional symmetry?
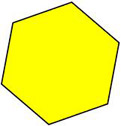
The correct answer is A. This figure has rotational symmetry, point symmetry, and reflectional symmetry. The angle of rotation is 
. The fixed point is marked in red below; this is also the point
of symmetry.
Choice B has reflectional symmetry.
Choice C has no symmetry. Choice D has rotational symmetry with an angle of rotation of 
.
