In this lesson, you will study how to find the area of triangles and special quadrilaterals.
How do we find the area of a parallelogram?
The formula for the area of a rectangle is the product of its base and height. This can also be used to find the area of any parallelogram.
In any parallelogram ABCD, draw the segments from C and D perpendicular to the line containing AB.
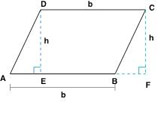
Call these points of intersection E and F, respectively. The length of either of the segments 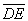 or
or 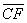 is the height, h. By the HL Theorem, triangle ADE and triangle BCF are congruent, and they therefore have the same area. From the figure, we see that the area of ABCD is equal to the area of the rectangle CDEF. So we have shown:
is the height, h. By the HL Theorem, triangle ADE and triangle BCF are congruent, and they therefore have the same area. From the figure, we see that the area of ABCD is equal to the area of the rectangle CDEF. So we have shown:
The area of a parallelogram is equal to the product of its base and its height: A=bh.
How do we find the area of a triangle?
Previously, we reviewed the following:
Each diagonal separates a parallelogram into two congruent triangles. Using this information and the formula for the area of a parallelogram, we can derive the formula for the area of a triangle:
The area of a triangle is one-half the product of its base and its height: 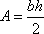 .
.
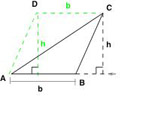
Given triangle ABC, with base AB = b and height h, draw the line parallel to 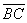 containing the point A. Choose a point D on this line so that DC = AB = b. By construction, ABCD is a parallelogram and
containing the point A. Choose a point D on this line so that DC = AB = b. By construction, ABCD is a parallelogram and 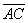 is a diagonal. Therefore, triangle ADC
is a diagonal. Therefore, triangle ADC  triangle CBA and the areas of these triangles are equal. If we call this area A, we have that:
triangle CBA and the areas of these triangles are equal. If we call this area A, we have that:
2A = area(ABCD) = bh. So we have proved 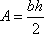 .
.
Question
Reveal Answer
The correct answer is C. To use the area formula, we need to determine the height of the triangle. From the previous section, we know that 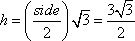 . This gives area
. This gives area 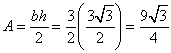
How do we find the area of a trapezoid?
An altitude of a trapezoid is any segment perpendicular to the bases . Its length is the height.
The area of a trapezoid is equal to one-half the product of its height and the sum of the lengths of its bases, b1 and b2:
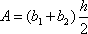 .
.
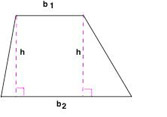
Question
What is area of the trapezoid shown below?
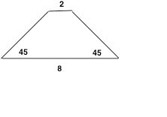
- 15
- 20
- 25
- 30
Reveal Answer
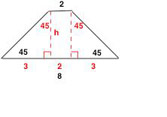
The correct answer is A . If we take the altitude shown below, then we can use that the resulting triangle is a 45-45-90 triangle along with the given information to get that h = 3. Using the formula, we get 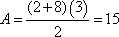 .
.
Review of New Vocabulary and Concepts
- If the sum of the measures of two angles is 180°, then the angles are called supplementary, and each angle is called the supplement of the other.
- If the sum of the measures of two angles is 90°, then the angles are called complementary and each angle is called the complement of the other.
- The angle bisector of angle BAC is the ray
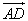 such that angle BAD
such that angle BAD 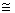 angle DAC.
angle DAC.
- Two lines that are not coplanar are called skew lines.
- A triangle is called scalene, isosceles, or equilateral according to whether it has no congruent sides, at least two congruent sides, or three congruent sides, respectively.
- A triangle is called an acute, right, or obtuse triangle according to whether it includes three acute angles, one right angle, or one obtuse angle, respectively.
- In a right triangle, the side opposite the right angle is the hypotenuse, and the other two sides are the legs.
- A median of a triangle is the segment from any vertex to the midpoint of the opposite side.
- An altitude of a triangle is the segment from any vertex that is perpendicular to the line containing the opposite side.
- Exterior Angle Theorem: An exterior angle of a triangle is equal to the sum of its remote interior angles.
- Two sides of a triangle are congruent if and only if the angles opposite those sides are congruent.
- A triangle has three congruent sides if and only if it has three congruent angles.
- If angle ABC is an isosceles triangle with congruent sides
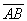 and
and 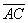 , then the median from A to
, then the median from A to 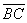 is the altitude from A to
is the altitude from A to 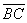 .
.
- HL Theorem : If the hypotenuse and one leg of a right triangle are congruent to corresponding sides of another right triangle, then the triangles are congruent.
- Ina 30-60-90 triangle, the length of the hypotenuse is twice the length of the shorter leg and the length of the longer leg equals the shorter leg times
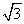
- In a 45-45-90 triangle, the length of the hypotenuse is
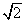 times the shorter leg.
times the shorter leg.
- The area of a parallelogram is equal to the product of its base and its height: A=bh.
- The area of a triangle is one-half the product of its base and its height:
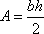 .
.
- The area of a trapezoid is equal to one-half the product of its height and the sum of the lengths of its bases, b1 and b2:
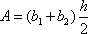 .
.
 username@email.com
username@email.com
![]() or
or ![]() is the height, h. By the HL Theorem, triangle ADE and triangle BCF are congruent, and they therefore have the same area. From the figure, we see that the area of ABCD is equal to the area of the rectangle CDEF. So we have shown:
is the height, h. By the HL Theorem, triangle ADE and triangle BCF are congruent, and they therefore have the same area. From the figure, we see that the area of ABCD is equal to the area of the rectangle CDEF. So we have shown:![]() .
. ![]() containing the point A. Choose a point D on this line so that DC = AB = b. By construction, ABCD is a parallelogram and
containing the point A. Choose a point D on this line so that DC = AB = b. By construction, ABCD is a parallelogram and ![]() is a diagonal. Therefore, triangle ADC
is a diagonal. Therefore, triangle ADC ![]() triangle CBA and the areas of these triangles are equal. If we call this area A, we have that:
triangle CBA and the areas of these triangles are equal. If we call this area A, we have that:![]() .
.![]() . This gives area
. This gives area 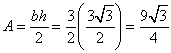
.
![]() .
.