Your Dashboard username@email.com
⬅ Previous Lesson Workshop Index Next Lesson ➡

The Equation of a Circle

Objective

In this lesson, you will determine the equation of a circle in the plane centered at a given point (h, k) with a given radius r. Also, given an equation of the circle, you will show how to find its center and radius.

Previously Covered:

  • Pythagorean Theorem : The square of the hypotenuse is equal to the sum of the squares of the non-hypotenuse legs in any right triangle.
  • Let P be a point in the plane and let r be a positive real number. The circle with center P and radius r is the set of all points in the plane with distance r from P.

How do we find the equation of a circle in the plane, given its center and radius?

Before answering this question generally, consider a special case. Suppose we have a circle of radius r centered at the origin. Let (x, y) be any point of the circle. The distance between (x, y) and (0, 0) is r, by definition of the circle. If (x, y) is not one of the four special points (r, 0), (–r, 0), (0, r), (0, –r), then we can always draw a right triangle with hypotenuse length r and legs of length x and y as shown below.

Circle with inscribed right triangle

So, by the Pythagorean Theorem, x and y satisfy the equation x2 + y2 = r2 . (Notice that the four special points satisfy this equation.) This is the equation of the circle of radius r centered at the origin.

Now, we can move the circle of radius r centered at the origin to any point (p, q) of the plane by two graphing transformations: a horizontal shift of x arrow x – h and a vertical shift of y  y – k. This gives us the equation (x – h)2 + (y – k)2 = r 2. We have shown the following:

The equation of a circle in the plane with center (h, k) and with radius r is: (x – h)2 + (y – k)2 = r 2.

Question

What is the equation of the circle shown below?

Circle on coordinate plane

Reveal Answer

The correct answer is A . The center is (–3, 0) and the radius is 4 . We use the form . This gives or .

If we expand this equation, we get another form for the equation of the circle called the standard form.

The standard form of the equation of a circle is .

Given the equation of a circle in its general form, how can we find the center and radius?

To find this information, we can reverse the process of expanding the center-radius form of the circle. This reverse process is actually the method of completing the square. Recall that . If we have the x2 and x terms, then to complete the square we need to add a constant term. But if we add a term, we need to add it to both sides of the equation to maintain equality.

In the case of a circle, we actually need to do complete the square twice, once for x and once for y.

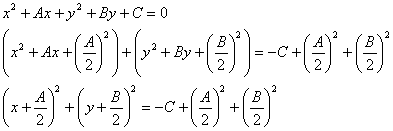
So the center of the circle is  and the radius .

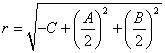Let’s try an example. What is the center of the circle given by the equation: ?

Step 1: Complete the square for the variable x.

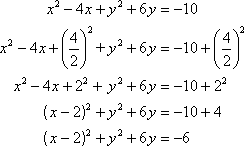
Step 2: Complete the square for the variable y.

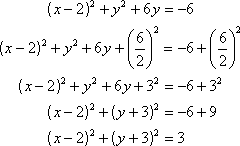
Step 3: Take the square root of the remaining term to get the radius.

The center is (2, –3) and the radius is  .

Question

What is the radius of the circle given by the equation ?

  1. 1
  2. 4
  3. 3
  4. 9

Reveal Answer

The correct answer is C . Complete the square as in the preceding example.

Because the equation of a circle with center (h, k) and radius r is , r = 3.

⬅ Previous Lesson Workshop Index Next Lesson ➡

Back to Top