Parallel & Perpendicular Lines

Objective

In this lesson, you will study the slopes of parallel and perpendicular lines.

Previously Covered:

The slope of a line equals
The equation of a line can be in either of these forms: ax + by = c, which is called standard form, or y = mx + b which is called slope-intercept form, where a, b, c, and m are real numbers.

What are parallel lines?

Parallel lines are lines in the same plane that do not intersect.

We use the symbol to stand for the words “is parallel to.”

So, given two lines, AB and CD, as shown below

$Two Parallel Lines$ then AB

CD.

Because parallel lines maintain the same distance from each other, their slopes must be equal. In their equations, the only difference between the two lines is in the y-intercept. Therefore, because the slope-intercept form of the equation of a line is y = mx + b, we might have the equation y = 3x + 4.

Another line that is parallel to the first might have the equation y = 3x – 10.

In both cases, the slope of the line (m) is the same.

A line that differs from another by its y-intercept only is called a vertical translation of the line.

For example, find the slope of a line that is parallel to 3y – 2x = 12.

Because the equation is in standard form, we must first put it into slope-intercept form. To do so, solve for y.

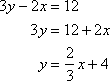
Because the two lines are parallel, both have a slope of

Now, write equations for two lines that have a slope of 2, given that one line’s y-intercept is at the point (0, 5) and the other line’s y-intercept is at the point (0, –8).

The equations must be in the form y = mx + b. Simply plug in the slope and y-intercepts of each line into the equation.

The first equation becomes y = 2x + 5 and the second line becomes y = 2x – 8.

Two lines are perpendicular to each other if their intersection forms four right angles. For example, a vertical line and a horizontal line are perpendicular. The slopes of perpendicular lines are negative reciprocals of each other. This means that the product of the two slopes is equal to –1. Thus, a line with a slope of 2 is perpendicular to a line with a slope of .

Given the line y = 3x + 4, determine the equation of a line that is perpendicular and has a y-intercept of 8.

Because the slope of a perpendicular line will be the negative reciprocal of 3, the slope of the new line is .

Because the y-intercept is 8, the equation of the new line is y = x + 8.

Workshop Index Next Lesson ➡