Finding the Equation of a Line

How do we locate a line on the coordinate plane?

The slope of a line indicates how steep it is. To locate a line on a coordinate plane, however, we must know at least one point on the line as well as the line’s slope.

Remember that the y-intercept is the value of y where the line crosses the y-axis. In other words, it is the value of y where x = 0. In the slope-intercept form of an equation, b is the y-intercept. Therefore, if we know the slope and the y-intercept, we are able to find equation of the line in slope-intercept form.

What if we know the slope and a point other than the y-intercept?

For example, we know a line contains the point (2, 3) and has a slope of 2. By plugging the slope into slope-intercept form we find that y = 2x + b.

Graph the point (2, 3). From there, move 2 units up and 1 unit right to find a second point.

In effect, we have substituted the values from the point we know into the slope formula.

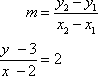
Then multiply both sides of the equation by (x – 2) and simplify to solve for y.

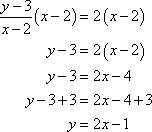
We now have the slope-intercept form of the equation, which was simplified from point-slope form of the equation in step two above. To generalize point-slope form, the equation of a line through a point (x₁, y₁) is ,where m is the slope.

What if we know the x– and y-intercepts, but not the slope?

If you know the x– and y-intercepts, substitute the values of those points into the formula for slope.

Then substitute the slope into slope-intercept form.

For example, given the points (12, 0) and (9, 1), find the equation of the line in point-slope form.

First, use the two points given to find the slope.

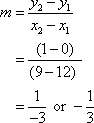
Then substitute the values of one point and the slope into the equation .

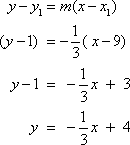
The slope is  and the y-intercept is (0, 4).

Review of New Concepts and Terms

• An equation is a statement that shows that two mathematical expressions are equal.
• In a linear equation, no variable has an exponent greater than one.
• An equation in the form ax + b = 0 is a linear equation in one variable. It is also called a first-degree equation in one variable. In standard form, a linear equation in two variables is in the form ax + by = c, where a, b, and c are constants, and not all are equal to zero.
• In a linear inequality, the symbol  means greater than,  means less than,  means less than or equal to, and  means greater than or equal to.
• The standard form of a linear equation is ax + by = c.
• The slope-intercept form of an equation is y = mx + b.
• 

Further Reading

Algebra Demystified: A Self-teaching Guide (Rhonda Huettenmueller): McGraw-Hill, 2003.

College Algebra (Ron Larson and Robert P. Hostetler): Houghton Mifflin, 2003.

Practical Algebra: A Self-Teaching Guide (Peter H. Selby and Steve Slavin): John Wiley and Sons, 1991.

Schaum’s Outline of Intermediate Algebra (Ray Steege and Kerry Bailey): McGraw Hill, 1997.

Don’t forget to test your knowledge with the Algebra and Functions I Chapter Quiz;