⬅ Previous Lesson Workshop Index Next Lesson ➡

Solving and Graphing Quadratic Equations

Objective

In this lesson, you will study two different forms of quadratic equations: standard form and vertex form. Also, you will study how to find the roots of quadratics both algebraically and graphically. You will be introduced to the concept of symmetry in graphs of parabolas.

Previously Covered:

Rational polynomials can be easily simplified when they are factored (if possible) and common terms are eliminated. Always look for a GCF before factoring.
The operations addition, subtraction, multiplication, and division can be polynomials to combine multiple rational polynomials into one final solution.
Rational functions are undefined at their asymptotes.

What is the standard form of a quadratic function?

The standard form of a quadratic function is , where a, b, and c are real numbers, and . Each term in the function has a special purpose:

is the quadratic term.

is the linear term.

c is the constant term.

The coefficient of the quadratic term, , determines how wide or narrow the graphs are, and whether the
graph turns upward or downward.

Important Tidbit

A positive quadratic coefficient causes the ends of the parabola to point upward.
A negative quadratic coefficient causes the ends of the parabola to point downward.
The greater the quadratic coefficient, the narrower the parabola.
The lesser the quadratic coefficient, the wider the parabola.

In this graph, coefficient a is positive and large. Therefore the parabola is narrow and points upward.

$Narrow parabola opening upward$

In this graph, coefficient a is smaller. Therefore, the parabola is wider.

$Wider parabola opening upward$

Here, coefficient a is negative, therefore the endpoints of the parabola point downward.

$Parabola opening downward$

The linear-term coefficient b shifts the axis of symmetry away from the y-axis. The direction of shift depends on the sign of the quadratic coefficient and the sign of the linear coefficient.

The axis of symmetry shifts to the right if the equation has:

positive a and negative b coefficients, or
negative a and positive b coefficients.

The axis of symmetry shifts to the left if the equation has:

positive a and positive b coefficients, or
negative a and negative b coefficients.

The constant term c affects the y-intercept. The greater the number, the higher the intercept point on the y -axis.

Question

Which graph best matches the quadratic function ?

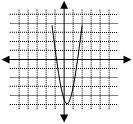
$Parabola with linear coefficient -2 that opens upward$
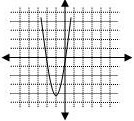
$Parabola shifted left that opens upward$
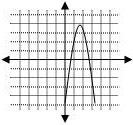
$Parabola shifted right, opening down$
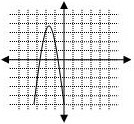
$Parabola shifted left, opening down$

Reveal Answer

The correct choice is A. The quadratic coefficient is +3, therefore the endpoints of the graph will turn upward. This eliminates choices C and D. The y-intercept is . A linear coefficient of –2 paired with a positive quadratic coefficient indicates the axis if symmetry will shift to the right.

What is the vertex form of a quadratic equation?

There are times when the minimum or maximum point of a parabola, called the vertex, is not located at the origin. When this is the case, we can write the quadratic function in vertex form, in order to easily identify the coordinate location of the vertex, and thus the axis of symmetry. Vertex form is .

The variables (h, k) are the coordinate location that determines the position of the vertex. The quadratic coefficient a determines the direction of the end points of the parabola.

Question

What is the equation of the quadratic function modeled in the following graph?

Reveal Answer

The vertex is located at (–2, 3), and a second point on the graph is located at (–4, –4). Therefore, h
= –2, k = 3, x = –4, and y = –4. You can now solve for a using the vertex form, as shown below.

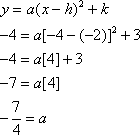
The quadratic function is . The correct choice is B.

How do we solve quadratic functions by algebraic methods?

When we solve quadratic functions, we are actually finding the roots of the equation. A root is a point where the equation is equal to zero (in algebraic terms), or where the graph crosses the x-axis (in graphical terms).

Method one: Solve by factoring.

Factor to solve the quadratic equation 14x² + 7x = 0.

Step 1: Factor out a GCF of 7x, and rewrite the equation as 7x(2x + 1) = 0.

Step 2: Since the first term, 7x, is multiplied by the second binomial, 2x + 1, we have to determine what numbers are required to make the equation equal zero. This gives us two equations.

Step 3: The roots are x = 0 and .

For example, use factoring to solve the quadratic equation .

Step 1: The quadratic factors into .

Step 2: Set each binomial term equal to zero, and solve.

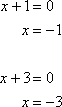
Step 3: The roots are and .

Method Two: Solve by completing the square

You are able to solve quadratic equations by completing the square because if you square a binomial, the result is a perfect square trinomial.

Binomial	Perfect Square Trinomial

The first step is to find the perfect square trinomial, and then write the trinomial as a binomial squared, using the following formula.

For example, solve by completing the square.

Step 1: Rewrite the quadratic equation with the terms containing x on the left side of the equal sign, and the constant on the right side of the equal sign.

Step 2: Divide the coefficient b by 2, square the result, and add this to both sides of the equation.

Step 3: Simplify. Notice that the left side is a perfect square trinomial.

Step 4: Take the square root of both sides, and solve for the roots.

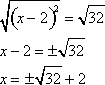
Method Three: Solve using the quadratic formula.

The quadratic formula is a straightforward method that always produces a solution, when other methods such as graphing, factoring, and completing the square require too much effort or are not easily done. The formula is

A part of this formula, called the discriminate, quickly provides valuable information about the roots. The discriminate is .

Important Tidbit

If is:

positive, there will be two real roots and no imaginary roots.
negative, there will be two imaginary roots and no real roots.
zero, there will be one real root.

For example, solve the equation .

Step 1: Identify the coefficients: a = 3, b = 2, and c = 1. Therefore, the discriminate is:

A negative under the radical means the solution will have imaginary roots.

Step 2: Apply the quadratic formula:.

Step 3: Simplify further, and write the solution in imaginary form.

Important Tidbit

Remember, for an imaginary number, .

Method Four: Solve quadratic equations by graphing

Graphing provides a visual way to easily identify the roots, and see how the equation behaves over a given domain and range.

For example, solve .

Step 1: Draw the graph, and identify where the parabola crosses the x-axis.

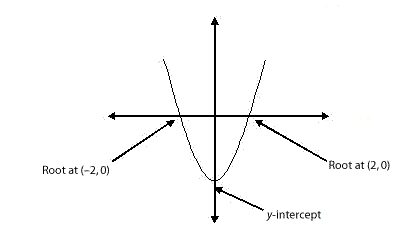
Step 2: The x-axis crossing points are the solution to the equation, where y = 0. Therefore, the roots are x = 2, and x = –2.

Important Tidbit

We could also write the solution as . If we multiply the binomials, the result is the original equation,

⬅ Previous Lesson Workshop Index Next Lesson ➡