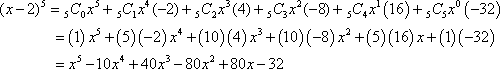username@email.com
username@email.com
In this lesson, you will study expanding binomials to any power using Pascal’s triangle and the Binomial Theorem.
In our previous discussion, we combined two binomials to produce a perfect square trinomial.
![]()
The process of raising a binomial to a power, and deriving the polynomial is called binomial expansion. The binomials are of the form ![]() .
.
It is not practical to manually expand binomials. There are just too many steps involved, and the chance of an error is too great to undertake this by hand (not to mention the time involved). Fortunately, there are methods available to help us bypass the tedious calculations and more quickly expand binomials of a higher degree.
A very simple and practical way to expand binomials is to use a diagram called Pascal’s Triangle.
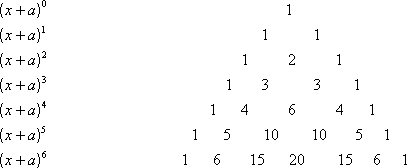
This is a diagram of the coefficients of the expansion. Notice the pattern in the triangle. Each number is the sum of the two numbers above it. For example, the central number in the ![]() row is 20. This is derived from 10 + 10, the two numbers it is centered below.
row is 20. This is derived from 10 + 10, the two numbers it is centered below.
Using this process, we can build Pascal’s triangle and use it to expand binomials to any degree.
For example, expand ![]() .
.
Step 1: From Pascal’s triangle, we see that the coefficients for a 5 th degree binomial are 1, 5, 10, 10, 5, and 1.
Step 2: We build the polynomial by first building each term. The exponent on the variable x starts with 5, and decreases by one each time. The exponent on the a-term starts at zero, and increases by one each time.
1st term: ![]()
2nd term: ![]()
3 rd term: ![]()
4 th term: ![]()
5 th term: ![]()
6 th term: ![]()
Step 3: Combine all terms, and write the final answer in standard form.
![]()
The Binomial Theorem is a more formal approach to binomial expansion. The Binomial Theorem
states that for positive integers n,
![]() .
.
The coefficients ![]() are combinations, and are calculated using the formula:
are combinations, and are calculated using the formula:
![]() .
.
For example, expand ![]() .
.
Step 1: Using the Binomial Theorem, we will first calculate the coefficients for each term.
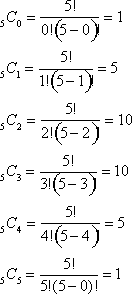
Notice how the coefficients are identical to the 5th
degree binomials in Pascal’s triangle.
Step 2: Write the binomial expansion using n = 5 and a = –2.