username@email.com
username@email.com
In this lesson, you will study more advanced algebra topics such as rational polynomials, factoring, quadratics, conics, exponents, and the Fundamental Theorem of Algebra.
is the input for the second function, 
. Composite functions are written as 
, then the inverse of the function contains the point 
.
, where m = slope and b = y-intercept. Any point on the graph of a linear equation is a solution to the equation.
point that is the solution to the system, if one exists. Not every system will have a solution.A polynomial is an expression that can be written as the sum of the terms 
where b is a positive integer.
The exponent on each variable is the degree of each term, and polynomials are usually written in standard form, meaning the terms are ordered in such a way that the degrees are placed in descending order.
For example,
This is a three-term polynomial written in standard form. The degree of the polynomial is the largest degree of its individual terms, which is 3.
Anytime a polynomial is written in standard form, the degree of the polynomial is just the exponent on the left-most term
What is the degree of the polynomial 
?
The correct answer is D. Because the polynomial is written in standard form, the degree is the exponent of the left-most term, which in this case is 6.
Which polynomial has a degree of 2, and is written in standard form?
The correct answer is B. All of the answers have a degree of 2, but only B is written in standard form with the terms in descending order by degree.
While there are no limits to the degree ad complexity of polynomials, we will focus on polynomials that have a degree of four or less.
and 
are examples of linear polynomials.
is an example of a quadratic equation.
is an example of a cubic polynomial.
is an example of a quartic equation.Polynomials can be further classified based on the number of terms. A polynomial with one term is called a monomial, a polynomial with two terms is a binomial, and a polynomial with three terms is a trinomial.
The following table helps clarify the difference between the classification by terms and degree.
Polynomial Classification |
||||
|---|---|---|---|---|
| Polynomial | Terms | Term Classification | Degree | Degree Classification |
 |
3 | Trinomial | 3 | Cubic |
| 2x + 1 | 2 | Binomial | 1 | Linear |
| -5 | 1 | Monomial | 0 | Constant |
 |
3 | Trinomial | 2 | Quadratic |
 |
2 | Binomial | 4 | Quartic |
To add or subtract polynomials, the like terms must be added or subtracted.
For example:
Multiplying polynomials requires distributing each term in the first polynomial to every term in the second polynomial, and then simplifying like terms. The process is easier when one of the polynomials is a monomial.
For example:
Multiplying a binomial and a trinomial is slightly more difficult.
For example:
To solve this problem, distribute each term in the first polynomial (2x-1), to every term in the second polynomial, 
.
Continue simplifying by multiplying the terms.
The final step is to combine like terms and write the polynomial in standard form.
Keep in mind the rule for exponents when multiplying like variables add the exponents together.
Multiplying two binomials is very common in algebra. FOIL is an acronym that can help you remember the steps in this multiplication process.
The letters in FOIL stand for “first, outside, inside, and last.” To multiply two binomials, multiply the first, outside, inside, and last terms of the polynomials, in that order.
First, write out the two binomials to be multiplied, placing them next to each other.
The first two terms in each binomial are 2x and x . Multiplying them results in 2x² .
The outside two terms are 2x and 1. Multiplying them results in 2x .
The inside two terms are 5 and x . Multiplying them results in 5x
The last two terms are 5 and 1. Multiplying them results in 5.
Next, add all terms that resulted from the FOIL multiplication.
To simplify into the final answer, combine all like terms. Remember that like terms have to have the same exponent on the variable.
Like multiplication, polynomials can be divided easily if there is a monomial involved.
For example:
Because the divisor is a monomial, each term in the numerator can be separated and divided by 2x.
Simplify each ratio to find the final answer.
Now try an example of dividing by a binomial.
This is still a relatively easy problem, because the numerator can be factored into two binomials, canceling out the denominator. (The next section will address factoring.)
Sometimes factoring and canceling cannot be used to solve a problem.
For example:
The quadratic does not factor with integer roots. Therefore, divide using long division.
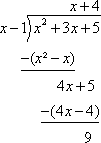
The final answer is 
.
Check the answer by multiplying each term by 
and working backward toward the original polynomial.
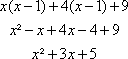
Because the new answer matches the original polynomial, the answer is correct.