username@email.com
username@email.com
In this lesson, we will prove the Pythagorean Theorem and its converse, and we will prove the formulas for special right triangles that were covered in a previous section.
Let P be a point in the plane and let r be a positive real number. The circle with center P and radius r is the set of all points in the plane with distance r from P.
A radius is any line segment from the center P to a point of the circle.
A chord of a circle is a line segment with endpoints on the circle.
The diameter of a circle is length of a chord containing the center of the circle and is denoted by d. The diameter of a circle is twice its radius.
In the figure below, AB, CD, and EF are all chords, but AB is the only diameter shown.
An arc is any connected segment of a circle. Any two distinct points A and B of the circle divide it into two arcs called the minor arc 
and the major arc
. In the figure below, the colored arc is the minor arc and the black arc is major arc .
Each minor arc of a circle has an associated central angle θ whose vertex is the center P and whose measure is less than 180°.
If the measure of θ is 180°, then A and B are actually endpoints of a diameter and the two arcs are semicircles.
The measure of minor arc is the measure of its associated central angle, the measure of a semicircle is 180°, and the measure of a major arc is 360° minus the measure of the corresponding minor arc.
If B is a point of the arc AC, then m(
) = m(
).
What is the measure of the minor arc
in the figure below if 
= 155° and m 
EPD= 15° ?
The correct answer is B . First note that 
=mEPD =15° . By the Arc Addition Theorem, 
°
An angle is inscribed in an arc if the sides of the angles contain the endpoints of the arc and if the vertex is a point on the circle touching the arc. In the figure below, 
ABC is inscribed in the major arc 
shown in color.
An angle intercepts an arc if the endpoints of the arc lie on the angle and each side of the angle contains an endpoint of the arc. In the figure below, each of the angles shown intercepts the arc 
.
Given an arc of a circle, what is the relationship of the corresponding central angle to a corresponding inscribed angle?
The measure of an inscribed angle is equal to half the measure of its intercepted arc.
We will prove a special case of this theorem, leaving the other cases as an exercise.
Let x denote the measure of the inscribed angle ABC.
There are three cases to consider:
Case 1: The inscribed ABC contains a diameter of the circle called AB.
Case 2: The points A and C are on the same side of a diameter containing B.
Case 3: The points A and C are on opposite sides of a diameter containing B.
Suppose we are in case 1 . Then the triangle PCB is an isosceles triangle, so m ABC = mPCB = x, as shown below.
Let y = 
denote the measure of the intercepted arc AC. The angles APC and CPB are supplementary, thus:
y + z = 180°. But, x + x + z = 180°, so y + z = 2x + z, or y = 2x.
What is the measure of the major arc 
?
The correct answer is D. The measure of the intercepted (minor) arc is equal to twice the measure of the inscribed angle, 2(80) = 160° . This means the measure of the major arc is 360 – 160 = 200°.
Two circles are congruent if they have congruent radii.
Two arcs are congruent if they lie on the same circle (or on congruent circles) and have the same measure.
The following two corollaries essentially follow from the definitions and the previous theorem; we will leave their proofs as an exercise.
If two inscribed angles intercept the same arc or congruent arcs, then the angles are congruent.
Two arcs in the same circle or congruent circles are congruent if and only if their corresponding chords are congruent.
What are tangent lines and secant lines?
A secant of a circle is any line intersecting the circle at two points.
A tangent of a circle is any line that intersects the circle at exactly one point called the point of tangency.
A line is tangent to a circle if and only if the radius drawn to the point of tangency is perpendicular to the line.
There are a number of theorems on the angles formed by secant and tangent lines, but we will just cover just two of them here.
The measure of an angle formed by two secants that intersect in the interior of a circle is one half the sum of the arcs intercepted by the angle and by its opposite angle.
Let 
and 
denote the secants and Q the point of their intersection . Let 1 be the measure of the angle formed by the secants. We need to show that 
.
Draw the chord 
and let 2 = QCB and 3 = QBC.
Because 
2 intercepts the arc
and 3 intercepts the arc 
we have 
and 
. Furthermore, m1 = m2 + m3. This gives the desired result .
The measure of an angle formed by an intersecting secant and tangent is one half the difference of the intercepted arcs.
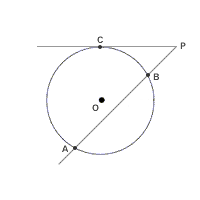
Based on this therom, if P denotes the angle formed by the intersection of secant AP and the tangent CP, then P=
.
Up to this point, we have only discussed the measure of arcs. But since arcs are, in fact, segments, they also have a length. Because an arc is curved, its length may seem more difficult to measure.
If we use the formula for the circumference of a circle and set up ratios, however, we can derive a formula for arc length.
The circumference of a circle is equal to 2
r, where r is the radius of the circle.
Because the circumference corresponds to an arc measure of 360 or 2 radians, the ratio of length s of an arc to the circumference C is equal to the ratio of the arc measure a to 2.
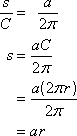
s = ar, where a is the arc measure and r is the radius of the circle.
What is the arc length in a circle of radius 3 corresponding to a central angle of 60?
The correct answer is C. In order to use the formula, we need to convert from degrees to radians.
radians
=
radians
By the formula for arc length, 
.