 username@email.com
username@email.com
In this lesson, you will study the classification of two- and three-dimensional solids using geometric properties such as number of vertices, edges, and faces.
The fundamental two-dimensional objects are polygons. Informally, a polygon is a figure created by fitting together a certain number of line segments.
A polygon is the union of n line segments P1, P2, P2, P 3, . . . P3, P1 such that P1, P2, . . . Pn is a sequence of n distinct points in the plane, with ![]() , satisfying the following properties:
, satisfying the following properties:
(1) No two segments intersect except at their endpoints.
(2) No two segments with a common endpoint are collinear.
A polygon with n sides is called an n-gon.
Which of these figures is not a polygon?
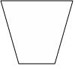
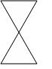

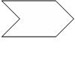
The correct answer is B. This figure does not satisfy condition (1) in the definition of polygon.
We can distinguish between polygons by counting the number of sides, or equivalently, the number of corners. This allows us to distinguish between different “shapes.” Below are examples of a 3-gon (or triangle) and a 4-gon (or quadrilateral).
A polygon is convex if no two points of it lie on opposite sides of a line containing a side of the polygon or more simplistically a polygon such that a line containing the side of the polygon does not cross the interior of the polygon. Polygons which are not convex are called concave polygons.
Which of the figures below is not a convex pentagon?

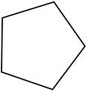
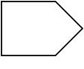

The correct answer is A. If we extend one of the two bottom sides, we can find points lying on opposite sides of an extended line or the extensions cross the interior of the polygon.
In the example above, all the convex figures have the more or less the same shape. So when we think about classifying figures by shape, we are really thinking about convex figures.
A polygon is regular if it is convex, all sides are congruent, and all angles are congruent. A regular octagon is shown below.
We can construct regular n-sided polygons for any positive integer n, where n is greater than or equal to 3. So there are infinitely many distinct regular polygons.
The analogue of a polygon in three dimensions is a polyhedron. A polyhedron is a three-dimensional figure made of up sides that are polygons. A solid polyhedron is the union of a polyhedron and its interior. The polygons are referred to as faces. The faces intersect in line segments called edges and the edges meet at points called vertices.
A convex polyhedron is a polyhedron such that no two points of it lie on opposite sides of a plane containing a face of the polyhedron. This implies that all faces of the polyhedron are convex polygons, Hence the polyhedron to the right below is convex. Another way to think of a convex polyhedron is that when you connect any two points on the polyhedron the segment formed must be contained on the polyhedron or in its interior.

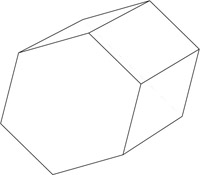
The simplest types of polyhedra are prisms. A prism is a polyhedron with two congruent polygonal faces contained in parallel planes. These faces are called the bases of the prism.
We can distinguish between two prisms by analyzing their bases.
Which of the following is not a hexagonal prism?
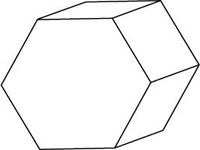
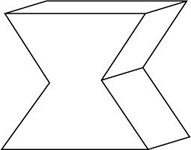
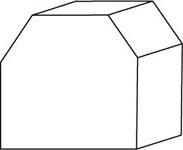
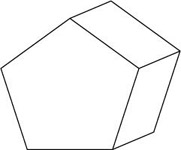
The correct answer is D . This is a pentagonal prism.
As was true for prisms, we can distinguish between different types of polyhedra by analyzing the faces and counting the faces, vertices, and edges.
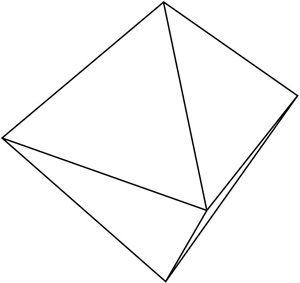
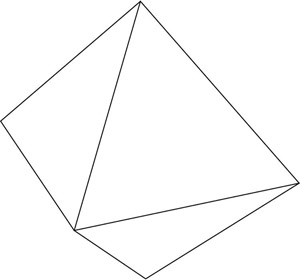
Suppose we are given two three-dimensional solids that are not prisms. Can we distinguish between a tetrahedron and a pyramid just by examining the shape of the faces? Sometimes we can.
A pyramid has one face that is a square, while the tetrahedron has triangles as faces.
We will need a bit more information to compare the hexahedron with an octahedron because both figures have only triangular faces. The polygon to the left below is the octahedron.
 |
 |
A count of the number of faces, edges, and vertices along with the shape of a face is usually enough to distinguish between any two solids.
For example, use this table to record the number of faces, edges, and vertices of a tetrahedron, cube, and triangular prism.
|
Vertices, Edges, and Faces of Solids
|
|||
|---|---|---|---|
|
Vertices
|
Edges
|
Faces
|
|
| Tetrahedron | |||
| Cube | |||
| Triangular prism | |||
|
Vertices, Edges, and Faces of Solids
|
|||
|---|---|---|---|
|
Vertices
|
Edges
|
Faces
|
|
| Tetrahedron | 4 | 6 | 4 |
| Cube | 8 | 12 | 6 |
| Triangular prism | 6 | 9 | 5 |
Notice that there is a relationship between the number of faces, edges, and vertices. In fact, any polyhedron satisfies Euler’s Formula: ![]() , where F = number of faces, E = number of edges, and V = number of vertices.
, where F = number of faces, E = number of edges, and V = number of vertices.
A polyhedron is regular if all its faces are congruent regular polygons, all of its dihedral angles are congruent, and the same number of faces meet at each vertex. The problem of classifying regular polyhedra is a very old problem, one studied extensively by the Greek philosopher Plato. The answer to this question is surprising in contrast to the analog in two dimensions. There are only five regular polyhedra, and they are referred to as the Platonic solids.
|
|
|
|
|
|
|
|
|