Conic Sections

Conic Sections

Intersecting a single or double cone with a geometric plane produces shapes called conic sections. In this lesson we will review three types of conic sections, or conics: circles, parabolas, and ellipses.

Circles

The standard form of the equation for a circle is

where r is the radius, (x, y) is the coordinate plane location for any point on the circle, and (h, k) is the coordinate plane location for the center of the circle.

The following graph shows a circle centered at the origin, with a radius of 2. The equation of the circle is .

The following graph shows a circle centered at (3, 2), with a radius of 2. The equation of the circle is .

Parabolas

Previously, we discussed parabolas and how they graphically reflect the behavior of quadratic equations. Now, we will look at the actual graphs themselves and some of the characteristics of parabolas in more depth.

Two parts of the graph that are important to identify are the directrix and the focus. The focus is a fixed point on the inside of a parabola, and the directrix is a fixed line on the outside of a parabola. The directrix is a line whose distance from the vertex is the same as the foci’s distance from the vertex. Any point on the graph of a parabola is the same distance from the focus as from the directrix.

The equation for the following graph is , where .The constant c identifies the location of the focus and directrix.

In this graph, the focus is located at (0, 3), therefore c = 3. The directrix is . The equation of the parabola is .

One example of a focus point that can be found in everyday objects is a flashlight. The bulb is seated at the focal point within the reflective surface, which is sort of like a parabola. Another example is a satellite dish. The receiver is located at the focal point, and the actual dish forms the shape of a parabola.

Parabolas can have four different configurations.

Open upward:
Open downward:
Open left:
Open right:

Ellipses

If a geometric plane intersects a single cone at an angle, the result is an ellipse.

The ellipse has two separate configurations, and therefore has two separate standard forms.

Major axis on the x-axis

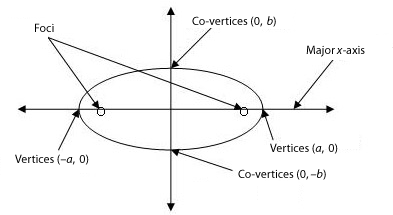
The standard form for an ellipse centered at zero with vertices on the x-axis and co-vertices on the y-axis is

Major axis on the y-axis

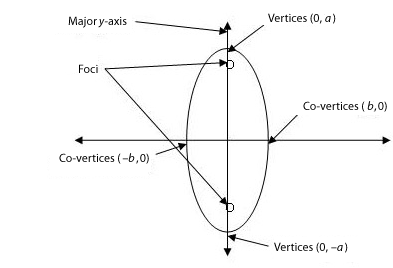
The standard form for an ellipse centered at zero with co-vertices on the x-axis and vertices on the y-axis is

Step 1: Write the equation in standard form. To convert the equation to standard form, divide each term by 400.

Step 3: Since y is the major axis, the vertices are located at (0, 5) and (0, –5). The co-vertices are located at (–4, 0) and (4, 0).

Review of New Vocabulary and Terms

• There are numerous ways to solve quadratic equations:
  • graphing,
  • factoring,
  • completing the square, and
  • using the quadratic formula.
• There are two forms of a quadratic equation, standard form and vertex form. The vertex form is used to easily identify the coordinate location of the vertex.
• The real-number solution to a quadratic equation is the point or points where f(x) = 0.
• Roots of quadratic equations can be either real or complex.
• Binomials can be expanded using two methods:
  • Pascal’s triangle – Pascal’s triangle is an efficient way to generate the coefficients in the binomial expansion.
  • The Binomial Theorem – The Binomial Theorem requires knowledge of computing combinations, using factorials.
• Intersecting a single or double cone with a geometric plane produces shapes called conic sections such as circles, parabolas, and ellipses.
• The focus point and directrix of a parabola are the same distance away from the vertex.