 username@email.com
username@email.com
We will cover the formulas for the sum of the interior angles and the sum of the exterior angles for convex polygons. We will use these formulas to solve related problems, such as determining when two convex polygons are similar or congruent .
At this point, we know how to show that two polygons (that are not triangles) are congruent or similar is by verifying the respective definitions directly.
Which of the figures below are congruent?
The correct answer is A. Figures C and E are congruent, or identical. The pairs of figures A and F and figures B and H are both similar. In fact, any two regular n-gons are similar.
Let’s first answer the question for regular polygons. Although it may seem obvious to you, we have not yet proved the following fact.
Two regular polygons with the same number of sides are similar.
By definition, a regular polygon has congruent sides and congruent angles. Therefore, a pair of regular polygons with n sides automatically satisfies the definition of similarity. If the side length of the first polygon is d and that of the second polygon is e, then the ratio of similarity is d:e.
One approach to studying complex geometric figures is to break them into simpler pieces. The figure below shows this division for polygons with n ![]() 4, using diagonals.
4, using diagonals.
A line segment whose endpoints lie on two nonconsecutive vertices of the polygon is called a diagonal.
In the figures above some of the diagonals are shown in blue.
We can determine the answer to this question by a clever use of diagonals. We divide a convex polygon with n sides into (n – 2) triangles. Divided in this manner, the sum of the measures of the polygon is the sum of the (n – 2) triangles This gives a total of 180 (n – 2). We have proved the following:
The sum of the measures of the interior angles of a convex polygon with n sides is 180(n – 2).
Which choice shows the measure of an interior angle of a regular octagon?
The correct answer is A. By the formula above, the sum of the interior angles of a octagon is 180(6)=1,080°. Since a regular octagon has equal angles, an interior angle has measure ![]() .
.
Although the idea of a polygon’s interior angle is an obvious one, the idea of an exterior angle may not be so obvious . The exterior angle of a polygon is the angle formed externally between two adjacent sides or the angle formed on the outside of the polygon by the extension of a side of the polygon.
We can find a formula for the sum of exterior angles using the sum of the measures of interior angles for a convex polygon with n sides. In the diagram shown below, the interior and exterior angles at each vertex are supplementary, which means they add up to equal 180°.

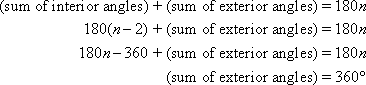
The sum of the measures of the exterior angles of a convex polygon with n sides is 360. Strangely enough, this result does not depend on the number of sides of the polygon.
If the measure of an interior angle of a regular n–gon is 156°, which choice shows the value of n?
The correct answer is C. There are two ways to solve this problem. Since the n-gon is regular, the interior angles all have the same measure. Therefore, all exterior angles have an equal measure. An exterior angle has measure 180-156=24°. So, using the formula for the sum of exterior angles, we get ![]() , or
, or ![]() . We can also use the formula for the interior sum.
. We can also use the formula for the interior sum.
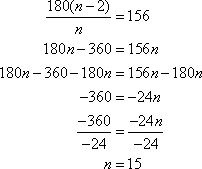
We can use the formulas on the sum of the measures of interior and exterior angles to solve problems relating to congruence and similarity. If we are given the measures of (n – 1) of the angles in a polygon with n sides, we can find the last angle using the formula.
Which of the following statements is true?
The correct answer is B. Each pair of corresponding sides has ratio 3:2, and because three pairs of the angles are congruent, the last pair is congruent by the interior angle sum formula.