username@email.com
username@email.com
In this lesson, you will cover the definition of a derivative and apply it to the evaluation of slopes and tangent lines of curves, instantaneous rates of changes of functions, relative maxima and minima, and methods to compute the derivative of several types of functions.
but not for numbers slightly lower, the function has a right-hand limit, and we say that 
exists.
as 
approaches 
. This is represented graphically with a vertical asymptote at 
.
approaches . For example, if 
, the limit at infinity is represented with a horizontal asymptote at 
.
in the interval (except the endpoints if the interval is open), 
, and terms both to the left and right of the equal sign exist.A derivative is nothing more than a special type of limit. However, it has many important applications and interpretations. Substitute 
for 
in our limit equation. We usually denote the derivative of 
as 
and define it as:
.
Given 
, where 
are constants, compute 
.
We will use the above limit to compute the derivative. First, we need to compute 
.
Therefore, 
. Hence, 
. Finally, we simply plug in values to find the derivative.
. We will use this derivation for a couple of examples, so keep this solution handy.
Let 
, where 
is a constant for all values of 
. That means 
as well. Therefore, 
. So the derivative of a constant is zero.
Compute 
for
(A) 
; and
(B) 
.
Hint: Remember the two limits for 
and 
for small values of 
. Also, recall the following trigonometric identities:
(A) 
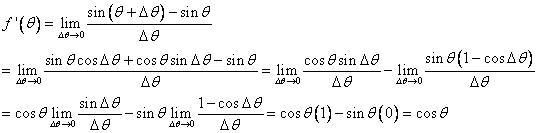
(B) 
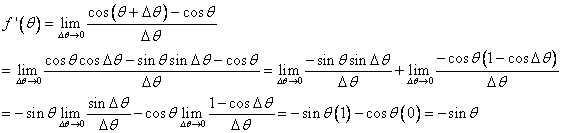
These two derivatives are significant to many applications in calculus and should be memorized.
The derivative of 
is 
.
The derivative of 
is 
.
If a function is in the form 
, recall that the graph crosses the y-axis at the y-intercept 
and has a constant slope 
.
The concept of slope is not limited to straight lines. Curves can have slopes as well, but the value of the slope of the curve 
changes as 
varies. As you may have guessed by now, the slope of the curve 
at any point 
is defined by 
. (Actually, the slope is not always defined; at these points, the value of 
is not defined.) Below we will show why.
Consider the curve below and the line intersecting the curve at points 
and 
.
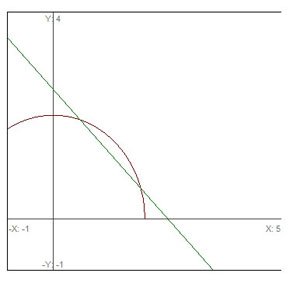
A line that intersects the curve at two points is known as a secant line. The slope of that line is given by:
Here, we define 
. Therefore, we can rewrite the above equation as:
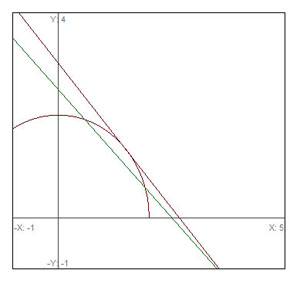
Let’s re-examine the above graph with another line that intersects the curve at just one point. This new line is known as the tangent line at the point of intersection, and describes the slope of the curve at that point. As you can see, it does not have the same slope as the secant line.
Imagine shifting the secant line so that the points of intersection become closer and closer to the tangent point. The slope of the secant line is still described by the above equation, but the value of 
gets smaller and smaller. In fact, the slope of the secant line and tangent line become identical as 
. We cannot simply plug in 
, because it would result in a zero in the denominator. What we can do, however, is consider the limitof the value of 
as 
approaches zero.
, which is precisely the value of 
.
For example, given 
, what is the slope of the curve at 
?
The graph of 
and its tangent line at 
are depicted below.
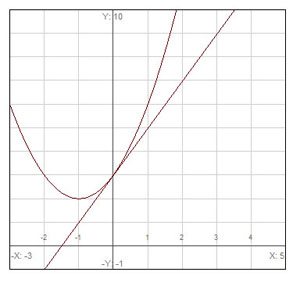
It appears that the tangent line intersects the x-axis at 
and the y-axis at 
. From these points, it appears that the slope is 
. We can verify this by taking the derivative of 
and plugging in 
. We already calculated the derivative: 
. At 
, 
.
Now that we understand that the derivative of a function is equivalent to the slope of a function at a point (or to the entire function, if the function describes a line), it should be easy to equate it to a rate of change. Recall that the slope of a line is defined as 
. In this form, the slope describes the rate of change in 
with respect to 
. In physics applications, we associate the words rate of change with time. In economics, rate of change might be associated with the rate of change of cost (such as marginal cost).
Let’s start with a physics example. Suppose the position of a particle over time can be described by the equation 
, where 
is measured in meters and 
in seconds. At time 
, the particle is at a position 
(think of a race car starting 
meters behind the starting line). Also note that, as 
increases, the value of 
not only grows, but grows at a greater and greater rate (we usually do not look at 
.
For example, what is theaverage velocity of the particle from 
to 
seconds? Recall from algebra that rate (velocity) = distance/time. Between 
and 
seconds, the particle has moved from position 
meters to 
meters, for a total of 
m. This distance is covered over a period of 
seconds. Therefore, the average velocity is 26/2 = 13 meters per second.
at 
seconds?We see that the average velocity over a time 
is described by:
. 
and 
sec. What happens as 
gets smaller and smaller? We can then measure the small change in position over a small interval in time. The average velocity then becomes close to the instantaneous velocity around that time. The instantaneous velocity is 
as 
approaches zero, or:
. Note that this is the formula for a derivative. Except we now use 
instead of 
, and the variable is 
instead of 
. We can therefore denote 
by the terms 
or 
. Rather than expand the limit term, let’s just borrow what we found in the first example. For the function 
, we found 
. Just substitute 
, 
, and 
(as well as changing 
to 
and 
to 
). We find: 
. This equation describes the instantaneous velocity at all times. At 
second, 
meters per second.
The acceleration is defined as the change in velocity over time. Using similar reasoning to find the instantaneous velocity, the acceleration 
is computed by taking the time derivative of the velocity:
Since 
, we can substitute 
, 
, and 
into the example formula to find 
. If you are familiar with physics, you may recognize 
as an approximation for the acceleration due to gravity.
A function 
is continuous at the value 
if and only if the following three rules hold.
exists.
exists.
A function is discontinuous along an interval if there are any breaks in the graph. If the value of the function shifts at a point, if the function is not defined at a point, or if the function increases or decreases without bound at a point (as indicated by a vertical asymptote) the function is discontinuous.
The slope (i.e. the derivative) of a curve is not always defined at all points on a continuous curve. A classic example of this is the absolute value function. Below is a graph of 
.
What is the value of 
at 
? It is clear that the function is defined at 
. The derivative is a limit, and this limit must be defined in an open interval around the point 
. However, no matter how small we make the open interval around 
, the slope of the curve in the portion of the open interval to the left of 
will always be a negative number, and the slope of the curve in the portion of the open interval to the right of 
will always be a positive number, so the limit is not defined since the limit from the right hand and left hand sides do not agree. You can also see this graphically. The tangent line must intersect the curve only at one point: 
. Prove to yourself that there are an infinite number of lines, all with different slopes, which could be described as a tangent line (any line that touches 
but does not penetrate the ‘V’). Be wary whenever you see a sharp turn or “pointy” graph when evaluating derivatives because the derivative will not exist at these sharp points or “cusps”.
Another example of an undefined derivative is at a point of discontinuity. If a function is discontinuous at a point, there is no derivative at that point.
Some functions are not differentiable at a certain point because the derivative increases or decreases without bound. One example is 
. Below is the graph of 
around 
.
At 
, the slope becomes infinite or vertical, so 
is not defined there. In fact, we will later prove that any function 
, where 
, will have an undefined derivative at 
.
We see that a function can be continuous at all points, while 
can be discontinuous at a point. This is , evidenced by “pointy” functions such as and functions whose derivatives have a vertical tangent line at a point such as 
. However, if a function 
is differentiable at 
, then it is also continuous at 
. In other words, differentiability always implies continuity, but continuity does not always imply differentiability.
If two functions 
and 
are differentiable, the following rules apply.
These rules are proven below.
Proof for rule 1:
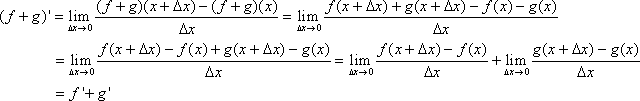
Proof for rule 2:
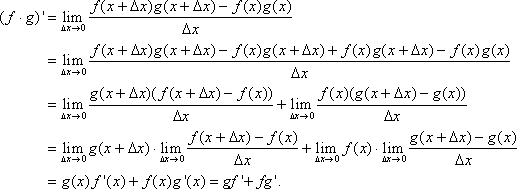
We can prove rule 3, or the quotient rule, using the limit definition of derivatives as well. However, the quotient rule can be derived from the product rule (rule 2), by changing 
to 
. Once we learn the general rule for differentiation of powers and an important rule for the derivative of composite functions known as the chain rule, the quotient rule can be easily derived from the product rule. Hence, it may not be necessary to memorize the quotient rule.
Before we proceed with examples, let’s learn three more important rules for derivatives:
is a constant, then 
.
, then 
, for n ≠ 0.
, where 
is positive, then 
.Proof for rule 4:
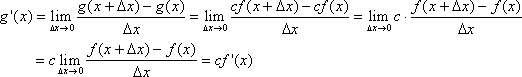
Proof for rule 5:
We can factor (x + Δx)n by using the Binomial Theorem.
Look carefully at the numerator. You can see that the term in parentheses breaks down into an xn-term (which cancels out) and a series of terms with 
etc. Since we divide the numerator by 
, the only term we are interested in is the 
-term. All the others will have 
to some power 
. Since the limit is for 
, all these will zero out. What we are left with is the coefficient in front of 
. According to the Binomial Theorem, that term is 
. Therefore, 
.
Proof for rule 6:
Applying the quotient rule and the power rule (rule 5) we just derived, we find that
Let’s try an example. Given 
, compute 
.
We will apply several of the above rules to solve this derivative. First, rule 1 tells us that we can treat each of the 4 terms separately. We won’t need to separate terms like this in the future, but for now:
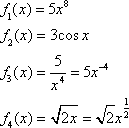
Therefore, 
.
The first term can be solved by combining rules 4 and 5.
The second term uses one of the memorized trigonometric derivatives.
.
The third term combines rules 4 and 6.
The fourth term is easier to solve with the 
-term separated from the variable.
.
Therefore, 
.
Let’s try another example. Given 
, compute 
.
One method to compute 
is to factor the terms and derive a single polynomial expression. However, we can also use the product rule. Let 
, and 
. Terefore, 
, and 
.
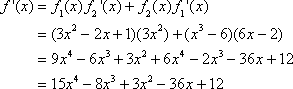
Try one final example. Let 
. If at least one of the terms can be expressed as 
, where 
is a constant and 
, show that 
is not differentiable at 
.
The derivative of 
is the sum of the derivatives of the terms, including 
. From rules 
and 
, 
, where 
is a constant. Since 
, 
. That means the exponent in the derivative expression is negative. Therefore, we can rewrite the derivative as 
, where 
is a positive number. At 
, 
does not exist, since we have division by zero. Since at least one term in the function is not differentiable, the whole expression is not differentiable.
A composite function is a function of a function. Given two functions 
and 
, the composite function is often denoted as 
or 
. For example, the function 
can be considered a composite function 
, where 
, and 
. Alternatively, we can have 
and 
. Another composite function is 
, where 
, and 
.
According to the chain rule, the derivative of a composite function 
is 
.
A couple of conditions apply to this rule.
, such that 
is defined, 
is also defined.
are differentiable functions.Here is another way to write the chain rule.
Let 
, and 
.
, and 
.
Therefore, we write the chain rule as 
.
Before we prove the chain rule, let’s do an example. Given 
, find 
. Recalling the rule for the derivative of powers, you might be tempted to say 
, but this would be incomplete. According to the chain rule, we must now multiply this term with the derivative of the term inside the parentheses. To clarify this, let 
. Therefore, 
, so 
, and 
. According to the chain rule,
.
After enough examples applying the chain rule, it should become second nature. It is similar to taking the derivative of the outside function and multiplying it by the derivative of the inside part. The chain rule will be used to calculate derivatives of trigonometric, logarithmic, exponential, and other function types, once we learn how to compute their derivatives.
For this proof, we will assume 
. This assumption is not necessary for the chain rule, but it makes it simpler to prove. Many calculus textbooks extend the proof for the case 
.
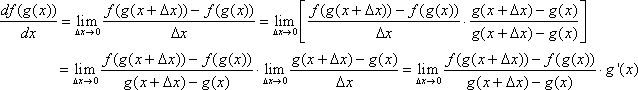
Since 
is differentiable, we know it is also continuous. Therefore, as 
, 
. Now we define 
. Note that
.
Therefore, 
, so we can continue our proof.
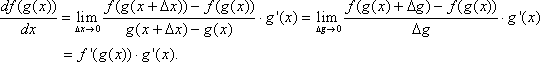
Let’s try a few more examples applying the chain rule. See if you can solve for the derivative without breaking the composite function into two functions.
In finding the derivative of 
, 
In finding the derivative of 
, 
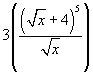
Here is another more complicated example below:
Given 
, find 
. You may want to break up the composite function in this example, because it is more complicated. Let 
, so 
, and solve 
.
and 
can be solved using the quotient rule.
Therefore, 
but not for numbers slightly lower, the function has a right-hand limit, and we say that 
exists.
as 
approaches 
. This is represented graphically with a vertical asymptote at 
.
approaches . For example, if 
, the limit at infinity is represented with a horizontal asymptote at 
.
in the interval (except the endpoints if the interval is open), 
, and terms to both the left and right of the equal sign exist.
is 
.
is 
.
is 
. Then apply the chain rule.
.
). 
.