username@email.com
username@email.com
In this lesson, you will cover the definition of a derivative and apply it to the evaluation of slopes and tangent lines of curves, instantaneous rates of changes of functions, relative maxima and minima, and methods to compute the derivative of several types of functions.
but not for numbers slightly lower, the function has a right-hand limit, and we say that 
exists.
as 
approaches 
. This is represented graphically with a vertical asymptote at 
.
approaches . For example, if 
, the limit at infinity is represented with a horizontal asymptote at 
.
in the interval (except the endpoints if the interval is open), 
, and terms both to the left and right of the equal sign exist.Up to this point, we have differentiated functions defined as 
. In other words, 
is defined explicitly in terms of the variable 
. There are situations where we define 
in terms of a third variable, or parameter, such as 
. In order to find 
, we apply parametric differentiation. Similarly, we may have an equation (not necessarily a function) that relates 
, but is not in the form 
. An example is the equation of a circle with a radius 
, centered about the origin: 
. We find 
through a similar technique known as implicit differentiation.
The rule for parametric differentiation is simple:
If 
, we can find 
by solving the ratio 
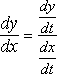, where 
.
This is actually a consequence of the chain rule.
For example, suppose x = t3 + 4t – 1, and y = 6 – t2. Use parametric differentiation to find 
.
If we were to solve this using only the tools we had in the last section, we would have to find a formula for 
in terms of 
(which may be next to impossible) and substitute that formula into the equation for 
, so we would be left with an expression for 
.
However, parametric differentiation makes this much easier:
.
If, as in this case, the formula for 
cannot easily be defined in terms of 
, you can create a table of values for 
.
This should provide information on the relationship of 
to 
. Some problems simply provide the 
value.
Given the equation of a circle, 
, with constant radius 
, use implicit differentiation to solve for 
.
Without implicit differentiation, we can solve for y.
We have two separate functions, one for the top semicircle, and the other for the bottom semicircle. We can then use the chain rule to solve for both values of 
.
Now we will examine how to use implicit differentiation. First, since both sides of the equation are equal, their derivatives are equal. Also, recall that the derivative of the left side of the equation is the same as the derivative of each of the two terms. To find 
, we will take the derivative 
of all three terms.
Therefore, 
. (The second term uses the chain rule since y is indeed dependent upon x, and the third term is 
because 
is a constant with respect to x).
We actually have two solutions for 
, depending on whether we are interested in the upper or lower semicircle.
The first equation describes the slope of the upper semicircle of a circle of radius 
centered about the origin, while the second equation describes the slope of the lower semicircle.
Using the tools of implicit differentiation, we are able to use differential calculus for applications known as related rates of change. We will solve two classic related rates problems: the sliding ladder and the leaking container.
A 10-foot ladder is leaning at an angle against a wall, with the foot of the ladder on the floor. The foot of the ladder is sliding across the floor at a rate of 
feet per second. When the foot of the ladder is 
feet from the wall, how fast is the top of the ladder sliding down the wall?
The wall, floor, and ladder form a right triangle, so we will use the Pythagorean Theorem to solve. The equation is 
, where 
is the distance from the wall to the foot of the ladder, 
is the height from the floor to the top of the ladder, and 
is the length of the ladder, which we know is 10 feet. We are asked to find the rate at which the top of the ladder is sliding down the wall, which according to our choice of variables is equivalent to 
. Be careful when you approach problems such as this, as we could have been asked to find the rate at which the bottom of the ladder is sliding across the floor. In that case we would be looking for 
. Since we are interested in changing rates over time, we take 
of all terms.
Therefore, 
.
At the beginning of this problem, we identified that we are looking for 
, so we will use this equation, and isolate that particular term. Solving for 
, 
. We are given 
, and 
feet per second. We still need to find the value of 
. That can be determined by using the Pythagorean Theorem again. 
, which gives us 
feet as the only positive answer. Therefore, 
feet per second. Note that the answer is negative, since the ladder is sliding in the 
direction.
A paper cup in the shape of a right circular cone has a height of 
inches and a radius of 
inches at its rim. It is filled with water, but develops a leak out of the bottom, at a rate of 0.1 cubic inch per minute. At what rate is the height of the water dropping when the cup is filled to a height of 3 inches?
In order to solve this problem, you need to know that the volume of a right circular cone is 
, and, according to the law of similar triangles, the ratio 
is constant at all heights. From this, we eliminate 
in the volume equation.
We are given 
and need to solve for 
, or the rate at which the height of the water is changing with respect to time. The first sentence tells us 
, so 
. Therefore, 
. Taking 
of both sides, we find
, or 
We are given 
and 
. Therefore, 
inches per minute.
The derivative 
is known as a first derivative of 
, or the first derived function. A derivative of a derivative is known as a second derivative function. One way a second derivative is denoted is 
, which is read, “
double prime.” We actually computed a second derivative earlier, when we calculated the acceleration in the example of a moving particle.
Recall that we found the velocity 
by taking the derivative of the position 
: 
, and then found the acceleration g by taking the derivative of the velocity, 
. We see that 
.
Another way to write the second derivative function is
Typically, third derivative functions also use primes, such as 
. Beyond that, we typically put the order in parentheses, like this: 
.
Alternatively, we can use the notation 
, which does not use parentheses. Power functions may eventually reach a point where higher-order derivatives are all zero. Other functions, like trigonometric, logarithmic, and exponential functions, can have infinite orders of derivatives.
Let’s try an example. Compute all higher order derivatives of 
(until 
).
Let’s try another example. Let 
. Compute 
, and extrapolate an equation for 
.
To solve, rewrite 
.
Note that the higher order derivatives alternate between + and – . You may also notice another pattern — the 
order derivative has 
in the numerator and 
in the denominator. The alternating signs can be mathematically represented as 
. Therefore, the 
derivative of y is 
.
Try one final example. Given 
, compute 
.
We are being asked to find the second derivative of y, with respect to x. We need to use implicit differentiation, the chain rule, and the quotient rule to solve this problem.
First, find 
by taking 
of each term.
Next, solve for 
.
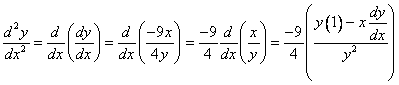
Next, substitute the value of 
into the above equation.
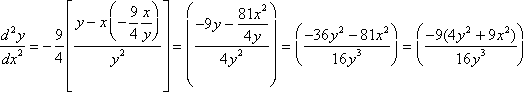
Finally, notice that due to some careful algebra, we have managed to write this last quantity in such a way that it contains the term 
. We know from the original problem statement that this term has a specific numerical value of 16 for that expression. When solving implicit differentiation problems on your own, look carefully for opportunities to use initial information like this. We now substitute 
for the value of 
.
?Before we proceed, we will define other key derivatives without proof. We are going to assume the reader is familiar with natural logarithms and exponential functions, as well as their properties.
If we know the derivative of 
, we can find the derivatives of other trigonometric functions. For example, it is easy to prove 
. Simply write 
, differentiate using the quotient rule, and utilize the trigonometric identity 
.
The following are important derivatives to know:
Do not forget that the chain rule can apply to any function. For example, 
. Derivatives for inverse trigonometric functions (e.g. 
) and hyperbolic trigonometric functions (e.g. 
) are beyond the scope of this module, but can be found in many calculus textbooks, math formula books, and are often provided as references when taking tests.
Two interesting rules apply in differential calculus when a function is continuous and differentiable on an interval. The first is Rolle’s Theorem.
Let 
be a function such that:
,
, and
.Then there is at least one number 
in (a, b) such that 
.
Of course, this is obvious if 
for all 
in 
. Since 
for all 
, any number 
in 
will satisfy 
.
We will illustrate Rolle’s Theorem with the graph 
( 
in degrees), on the interval 
and the interval 
. This function is both continuous and differentiable for all 
.
In the first graph, 
in the interval for 
and 
. According to Rolle’s Theorem, there must be at least one point in the interval where 
. That point is 
.
In the second graph, 
in the interval for 
and 
. According to Rolle’s Theorem, there must be at least one point in the interval where 
. That point is 
.
Now we can make a couple of observations about this graph. First, the line tangent to the point at which 
is always parallel to the x-axis. Second, the points at which 
appear to define some type of maximum or minimum of the curve in an interval. We will be discussing this second observation in great detail later.
Let’s try an example. The position of a ball thrown up in the air from the ground is described by the equation 
,
where 
is the upward velocity at 
, and 
is the downward acceleration due to gravity
(
are constant). At some time 
, the ball will strike the ground. Use Rolle’s Theorem to prove that, at some time 
, the velocity of the ball will be exactly 0.
You know from experience that when you throw a ball in the air, the position 
and velocity 
of the ball do not abruptly change at any time. Therefore, 
is continuous and differentiable. Also, we are given 
. Since all three conditions for Rolle’s Theorem are met, we know there is some time 
in the interval 
where 
. This time is when the ball reaches its peak height before coming back down.
Rolle’s Theorem is used to prove a very important rule in calculus known as the Mean Value Theorem.
Let 
be continuous on the closed interval 
and differentiable on the open interval 
. Then there exists at least one number 
in the open interval 
such that 
.
You may recall that we saw an equation similar to this when we interpreted the derivative in terms of a tangent line. It is the formula for the slope of the secant line connecting the points 
on the 
curve. We also know that 
is the slope of the curve at 
. Therefore, this theorem simply states that, for any secant line drawn on a curve, there is at least one point in between at which the tangent line is parallel to the secant line.
Since this curve meets the continuity and differentiability rules of the Mean Value Theorem, the point 
must exist somewhere in the 
interval.
Given the function 
over the interval 
, what is the value of 
that satisfies the Mean Value Theorem?
The correct choice is D. If we were to try to find 
whereby 
, we would first compute 
and 
. Therefore,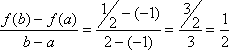 
. We compute 
, so we need to find 
such that 
. This is true when 
, which has no real solutions.
You might think that this example implies that the Mean Value Theorem is incorrect. However, this is not the case. Remember that 
must be continuous and differentiable in the interval 
, and 
is neither continuous nor differentiable at 
, which is in the open interval. Therefore, the Mean Value Theorem does not apply here.
When discussing how to determine limits in the previous module, we mentioned that there was a way to determine the limits of quotients in the form 
, which reduce to 
. This is known as L’Hôpital’s rule. There are two versions of this rule; the first is for the situation in which we find the limit of the quotient as 
, and the second for the situation in which we find the limit of the quotient as 
.
L’Hôpital’s rule for the indeterminate form 
:
If 
are functions that are differentiable for in an interval around 
(except possibly at 
), and both 
and 
, then if 
, where 
is a real number or , 
then 
.
L’Hôpital’s rule for the indeterminate form 
:
If 
are functions that are differentiable for in an interval around 
(except possibly at 
), and both 
and 
, then if 
, where 
is a real number or , then 
When written out formally, this rule sounds much more complicated than it really is. L’Hôpital’s rule is a method used to compute the limit of a function in which the variable is in the numerator and denominator. If plugging the value of the limit that 
approaches into the function leads to either 
, then just take the derivative of the numerator and the derivative of the denominator. Check out this new ratio. If you still get, 
, take the derivative again. Finally, whatever number you get as the limit, is the limit for the original function.
You can only use L’Hôpital’s rule whenever the limit is 
. Applying this rule to any finite, nonzero limit will produce an erroneous result.
Let’s try an example. Use L’Hôpital’s rule to prove the trigonometric limits that you were previously asked to memorize:
(A) 
; and
(B) 
.
(A) First, note that 
, so we know we can apply this rule.
The derivative of the numerator is 
, and the derivative of the denominator is 
. Therefore,
.
(B) First, note that 
, so we know that we can apply this rule again. The derivative of the numerator is 
, and the derivative of the denominator is 
. Therefore,
Let’s try a second example. Find 
.
By plugging in 
, you should find that both the numerator and denominator are 0 (
). Therefore, take the derivative of the numerator and denominator.
Again, plugging in 
leaves us with 
. Therefore, take the derivatives again.
Therefore, 
.
Let’s try one more example. Find 
.
First, note that the numerator and denominator both approach infinity as 
approaches infinity, so we have the indeterminate form 
. If we apply L’Hôpital’s rule, we find that 
. Note that the second term in the denominator approaches 0 at the limit, but the numerator and denominator still results in 
.
This means it is necessary to take derivatives again. You should see a pattern: the numerator will always be 
, the first term of the denominator will always have a power function that will go down by one, and the second term in the denominator will always approach zero as 
. Rather than take 
derivatives before the first term in the denominator fails to approach 
, you should see that the numerator will eventually win, so 
. The end result is that 
blows up more rapidly as 
than the 
and 
functions combined.
In previous sections, we have applied differential calculus to determine slopes of tangent lines and rates of change of functions. We will now introduce other useful applications. First, we will use differentiation as a tool for curve sketching.
From what we know about derivatives, we can look at the graph of a function and roughly determine its slope at all points. Wherever the curve’s y-value increases with increasing 
, we know its slope (hence its derivative) is positive. The steeper the climb, the larger the value of the derivative in that interval.
Likewise, a curve that decreases in an interval will have a negative derivative. At a point where a curve changes direction, the derivative is zero. We will illustrate this point in the following example.
For what values of 
is the function 
increasing and decreasing? Determine this by (A) computing 
, and (B) sketching the curve 
.
(A) 
. The curve 
increases in value whenever 
. Likewise, the curve decreases for all 
.
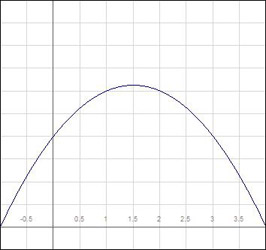
(B) The curve for 
is depicted below.
The curve clearly shows a parabola that decreases in value until 
, after which it increases. Note also that, at 
, 
. Earlier we saw that the line tangent to the curve at this point is horizontal.
For this curve, the point 
, at which 
, is an example of a critical point. This point, at which the curve changes from decreasing to increasing, is known as a local minimum. The local minimum is the point in the given interval at which the curve is at its smallest value. When a function changes from decreasing to increasing (or its derivative increases continuously from negative to positive), we say that the function is concave up, or has positive concavity.
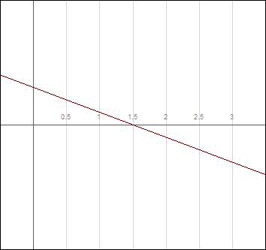
Now let’s examine the parabola 
below.
Its derivative 
. It also has a critical point at 
. However, it changes from increasing to decreasing at 
(i.e. its derivative changes from + to –). The point 
in the given interval, is known as a local maximum. Also, in this interval, the function is concave down.
Some books refer to convexity rather than concavity. Where a function has positive concavity, it has negative convexity, and vice versa. Some books also use the terms a relative maximum and minimum, rather than local maximum and minimum.
There is a third type of critical point, which is any point where a function is not differentiable. Thus, 
is a critical point for 
and 
.
For 
, use the first derivative test to find:
(A) over which interval the function is increasing and decreasing; and
(B) all local maxima and minima.
(A) 
. 
is increasing whenever the product 
. This occurs when either both terms are positive, or both terms are negative. Therefore, 
. The first condition is met whenever 
, and the second condition is met whenever 
. Another way to write this is that 
is increasing in the ranges 
. It should be obvious (or you can run through the entire argument) that 
is decreasing in the open range 
.
(B) The local extrema (the local maximum and minimum) are located at the points at which 
, which are the points 
. In the interval around 
, 
changes from positive to negative, which means 
is a local maximum. In the interval around 
, 
changes from negative to positive, so 
is a local minimum.
A graph of 
in the interval 
is depicted below.
![Graph of the interval [5, -5]](http://americanboard.org/Subjects/Images/math/8/images/Math%20Mod%208.3%20Art%20006.JPG)
We can see the local maximum and minimum and 
and 
, respectively. However, it is clear that the local maximum is not the largest value of the function in this interval, and the local minimum is not the smallest value. In the interval , the absolute maximum is at 
, and the absolute minimum is at 
. The first derivative test only identifies relative extrema, that is, the points at which the function shifts direction. Additional analysis is required to determine absolute extrema.
As we have learned, the first derivative of a function can be used to determine concavity (i.e. over what interval the function increases and decreases), and the location of relative extrema. We will call this analysis the first derivative test. We will now show that the second derivative test can be used to determine relative extrema and more.
Let’s look again at our two parabolas, 
and 
. We have already computed their derivatives, 
and 
. Below, 
and 
are sketched again.
 |
 |
 |
 |
Look carefully at their second derivatives, 
and 
. Note that the second derivative is always positive for 
and always negative for 
. This is illustrated below by graphs of the derivatives for 
and 
:
 |
 |
 |
 |
The second derivative is nothing more than the slope of the first derivatives. In the vicinity of a local minimum, the slope of the derivative (i.e. the second derivative) is positive; in the vicinity of a local maximum, the slope of the derivative (i.e. the second derivative) is negative. The same principle holds for any differentiable function where the second derivative exists.
If 
is differentiable on an open interval around 
, and 
exists, then:
(i) 
is a local minimum (and 
is concave up) if 
and 
;
(ii) 
is a local maximum (and 
is concave down) if 
and 
.
At this point, you may be wondering what happens when 
. Let’s look at two examples of this situation, 
and 
.
 |
 |
 |
 |
It is easy to show 
and 
. However, the point 
is neither a maximum nor a minimum for 
, and it is actually a relative minimum for 
. This tells us that the second derivative test does not always work. If the second derivative is zero, you may need to rely on the first derivative test to determine relative extrema and concavity.
For 
, the point at 
is known as a point of inflection. A point of inflection is any point along a curve at which the concavity changes directions from down to up or from up to down. In other words, the point 
is a point of inflection if 
when 
and 
if 
, or if 
when 
and 
if 
. The function does not have to be differentiable at this point, however. For example, we have seen that the function 
is not differentiable at 
. However, you can prove that 
satisfies the condition for a point of inflection at 
.
With what we know about maxima and minima, we are able to use the first and second derivative tests to solve optimization problems. We will demonstrate this with a couple of classic examples.
A rectangular field which runs to the bank of a straight river needs to be fenced off. There is a total of 2,000 yards of fencing material that can be used. Assuming the river forms one side, what is the maximum area that can be fenced in? Assume the field will have a length 
and width 
. The total area is 
. Let’s assume the river runs along the width. That means that the total amount of fencing material used is 
yards. Solving for 
. We then substitute 
into the equation of the area, and the result is 
. An extreme point occurs where 
. Therefore, A‘(x) = 2,000 – 4x = 0 or x = 500 yards, y = 2,000 – 1,000 = 1,000 yards, and the area is
A = (500)(1,000) = 500,000 square yards.
Is this the maximum or minimum area? The answer can be found by computing 
.
Since the second derivative is negative, this area is the maximum.
Let’s try another example. What is the area of the largest rectangle that can be inscribed within the parabola 
, as illustrated below? The x-axis defines the length of one side, and two corners lie on the parabola.
Assume the corners of the rectangle on the x-axis is at 
and 
. Therefore, the rectangle touches the parabola at 
, which is also the length of the rectangle. Therefore, 
. The extreme value for A is 
, or 
(we defined 
as positive). Therefore, 
and 
. Since 
for 
, we know this area is the maximum.
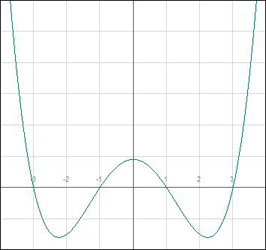
Another interesting application of derivatives is Newton’s method for approximating the roots of a function. The roots of a function are those points where the function crosses the x-axis, or where 
. They are also known as the zeros of a function. As an example, the function 
has four roots: 
. Below, we plot 
in a range where all its roots are visible, as well as the
vicinity of the root 
.
 |
 |
In the second graph, we also include the tangent line at 
. Let’s say 
is our initial guess of the root around 
. That initial guess is not accurate, but notice that the tangent line intersects the x-axis at a point much closer to the root (at about 
). Now, suppose you take the tangent line at 
. That tangent line will intersect the x-axis at a point even closer to the root (at 
). After a few iterations, you will come very close to the actual root.
Given 
, try 
as our initial guess for a root. The tangent line hits the curve at the point 
, has a slope 
, and we’ll say it crosses the x-axis at 
. With these two points and the slope, we can solve for 
.
Therefore, 
. With 
as our new guess, we can repeat the process.
It should be clear that, for the 
iteration:
Let’s try an example. Assuming an initial guess of 
, use Newton’s method to approximate 
.
The value 
is the positive root of the equation 
. Since 
, we have 
. We start with 
. You may want to use a calculator for these calculations.
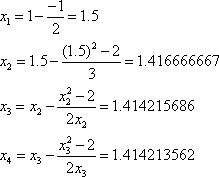
The value 
is as close to 
as a 10-digit calculator can calculate.
is expressed as 
.
can be interpreted as the slope of the tangent line of 
at 
, or the instantaneous rate of change of 
at 
.
.