 username@email.com
username@email.com
In this lesson, you will learn how to solve and apply elementary differential equations, convergence and divergence of sequences and series, differentiation and integration of power series, and Taylor series expansions of basic functions.
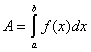 is a number rather than a function.
is a number rather than a function.A differential equation is an equation that contains derivatives. The order of a differential equation is the order of the highest ordered derivative in the equation. Thus, ![]() is a first-order differential equation, while
is a first-order differential equation, while ![]() is a second-order differential equation. A thorough study of differential equations is typically reserved for advanced calculus. This lesson examines elementary differential equations of the forms
is a second-order differential equation. A thorough study of differential equations is typically reserved for advanced calculus. This lesson examines elementary differential equations of the forms![]() and
and ![]() , where
, where ![]() is a constant.
is a constant.
Suppose ![]() represents a quantity such as a population of bacteria, the volume of a dye used in a medical analysis, the mass of a decaying radioactive substance, the future value of a compounded investment, etc. Then, the quantity
represents a quantity such as a population of bacteria, the volume of a dye used in a medical analysis, the mass of a decaying radioactive substance, the future value of a compounded investment, etc. Then, the quantity ![]() represents the growth of
represents the growth of ![]() . In these and other applications, the relative rate of growth is proportional to its quantity; that is,
. In these and other applications, the relative rate of growth is proportional to its quantity; that is, ![]() , where
, where ![]() is the constant rate of increase
is the constant rate of increase ![]() or decrease
or decrease ![]() in the quantity. Rewriting the equation as
in the quantity. Rewriting the equation as ![]() , we find
, we find ![]() , or
, or ![]() . Integrating both sides, we get
. Integrating both sides, we get ![]() . Therefore,
. Therefore, ![]() . This equation has the solution
. This equation has the solution ![]() where
where ![]() is a positive constant. Therefore,
is a positive constant. Therefore, ![]() where
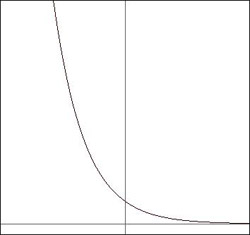
where ![]() can be any real number. This equation describes exponential growth and decay, which is represented graphically below for
can be any real number. This equation describes exponential growth and decay, which is represented graphically below for ![]() and
and ![]() respectively.
respectively.
 |
 |
There are an infinite number of solutions to this differential equation, as the choices for ![]() and
and ![]() are infinite. Typical physical problems, however, have a single solution. This is rectified by specifying initial conditions, such as
are infinite. Typical physical problems, however, have a single solution. This is rectified by specifying initial conditions, such as ![]() where
where ![]() and
and ![]() are given or measured.
are given or measured.
Let’s try some examples. The rate of growth of a bacteria culture is proportional to its population. Initially, the population is 10,000, but it increases to 25,000 after 10 days. What is the size of the population after 20 days?
This is an exponential growth problem of the form ![]() , where
, where ![]() is the population after t days, and
is the population after t days, and ![]() . The general solution is
. The general solution is ![]() . At this point, we have an equation for the population with two unknowns. To find a unique solution, we are given two initial conditions: (i)
. At this point, we have an equation for the population with two unknowns. To find a unique solution, we are given two initial conditions: (i) ![]() , and (ii)
, and (ii) ![]() . Initial condition (i) gives us
. Initial condition (i) gives us ![]() or
or ![]() Initial condition (ii) gives us:
Initial condition (ii) gives us: ![]() Therefore,
Therefore, ![]() Taking the natural log of both sides.
Taking the natural log of both sides. ![]() , so
, so ![]() . Therefore,
. Therefore,
![]() is the unique solution for the population at any time t. After 20 days,
is the unique solution for the population at any time t. After 20 days,
![]()
Newton’s law of cooling says that the rate of change in temperature ![]() of an object is proportional to the temperature difference between the object and its surroundings. If the constant of proportionality is
of an object is proportional to the temperature difference between the object and its surroundings. If the constant of proportionality is ![]() , and the initial temperature is
, and the initial temperature is ![]() (A) find an expression for
(A) find an expression for ![]() in terms of
in terms of ![]() and
and ![]() , and (B) in terms of
, and (B) in terms of ![]() , how much time does it take for the temperature difference to be cut in half?
, how much time does it take for the temperature difference to be cut in half?
(A) Over time, the temperature of the object approaches the temperature of the surroundings; therefore, the difference decreases over time, so this is an example of exponential decay. We note ![]() for
for ![]() , so
, so ![]() . Our initial
. Our initial ![]() condition is
condition is ![]() so our expression for
so our expression for ![]() is
is
![]() .
.
(B) We want to find the time ![]() for which
for which ![]() . We find
. We find ![]() , so
, so ![]() . Therefore,
. Therefore,
![]()
The next differential equation we examine is the form ![]() or
or ![]() , where
, where ![]() is a constant. As a guess, assume a solution
is a constant. As a guess, assume a solution ![]() . We find:
. We find:
![]() ,
,
or
![]() ,
,
which satisfies the differential equation when ![]() . Although we chose a cosine function, this also applies to a sine function. The
. Although we chose a cosine function, this also applies to a sine function. The ![]() variable allows for the shift from cosine to sine. Since the cosine function repeats itself over time, this differential equation describes periodic motion or oscillations. We are typically interested in periodic and bounded motion, known as harmonic motion.
variable allows for the shift from cosine to sine. Since the cosine function repeats itself over time, this differential equation describes periodic motion or oscillations. We are typically interested in periodic and bounded motion, known as harmonic motion.
The ![]() -term is known as the angular frequency, measured in radian/sec. The term
-term is known as the angular frequency, measured in radian/sec. The term ![]() is called the phase of motion, and
is called the phase of motion, and ![]() is the phase constant. If we imagine an object moving in a circle of radius
is the phase constant. If we imagine an object moving in a circle of radius ![]() about the origin,
about the origin, ![]() is the angular displacement from the x-axis at
is the angular displacement from the x-axis at ![]() , and
, and ![]() is the angular speed of the object.
is the angular speed of the object.
Here is an example. Newton’s second law of classical mechanics states that a force ![]() acting on a constant mass
acting on a constant mass ![]() is proportional to the acceleration
is proportional to the acceleration ![]() of the mass,
of the mass, ![]() . Previously, we learned that acceleration is the second derivative of the position function; that is,
. Previously, we learned that acceleration is the second derivative of the position function; that is, ![]() (assuming we restrict motion to the x-direction). We also learned of Hooke’s law, which states that the force exerted by a spring that is displaced a distance
(assuming we restrict motion to the x-direction). We also learned of Hooke’s law, which states that the force exerted by a spring that is displaced a distance ![]() from its natural position is
from its natural position is ![]() , where
, where ![]() is a constant. Suppose a mass
is a constant. Suppose a mass ![]() attached to the end of a massless spring of spring-constant
attached to the end of a massless spring of spring-constant ![]() is placed on a frictionless surface and is initially stretched a distance
is placed on a frictionless surface and is initially stretched a distance ![]() from its natural position. (A) Show that the behavior of the spring-mass system is described by harmonic motion, and (B) find the angular frequency in terms of
from its natural position. (A) Show that the behavior of the spring-mass system is described by harmonic motion, and (B) find the angular frequency in terms of ![]() and
and ![]() .
.
(A) Setting both force equations equal to one another, we find ![]() , or
, or ![]() Since
Since ![]() and
and ![]() are both positive constants, the ratio
are both positive constants, the ratio ![]() is positive. This is in the form
is positive. This is in the form ![]() , and is therefore an equation for harmonic motion.
, and is therefore an equation for harmonic motion.
(B) From the equation ![]() , we know
, we know ![]()
A sequence is a function whose domain is the set of positive integers. Recall that the domain of a function ![]() is the set of all possible values of
is the set of all possible values of ![]() . For example, the sequence
. For example, the sequence ![]() has the reciprocals of all positive integers as its elements.
has the reciprocals of all positive integers as its elements.
If ![]() is a sequence, then
is a sequence, then ![]() is known as a series. Each
is known as a series. Each ![]() is a term of the series. Of special interest is an infinite series, where the number of terms is infinite. A geometric series is an infinite series where consecutive terms differ by the same ratio; the simplest form is
is a term of the series. Of special interest is an infinite series, where the number of terms is infinite. A geometric series is an infinite series where consecutive terms differ by the same ratio; the simplest form is ![]() , where
, where ![]() is constant. A power series is of the form
is constant. A power series is of the form ![]() (specifically, a “power series in
(specifically, a “power series in ![]() ”), and it will be given special treatment in this module.
”), and it will be given special treatment in this module.
Sequences and series can be convergent or divergent. The sequence ![]() is convergent if
is convergent if ![]() for some finite value
for some finite value ![]() . If
. If ![]() or cannot be defined (for example, if the sequence eventually settles into a pattern of oscillation between two distinct values) , the sequence is divergent. Likewise, an infinite series is convergent if the sum approaches a finite value, and is divergent if the sum blows up to
or cannot be defined (for example, if the sequence eventually settles into a pattern of oscillation between two distinct values) , the sequence is divergent. Likewise, an infinite series is convergent if the sum approaches a finite value, and is divergent if the sum blows up to ![]()
or cannot be defined. It is easily proven that, if an infinite series ![]() is convergent, then
is convergent, then ![]() Are the following sequences convergent or divergent?
Are the following sequences convergent or divergent?

(A) ![]() so we use L’Hôpital’s rule.
so we use L’Hôpital’s rule.
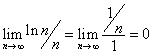
The sequence converges to ![]()
(B) ![]() so the sequence is divergent.
so the sequence is divergent.
(C) The sequence forever alternates between ![]() and
and ![]() , so it is divergent.
, so it is divergent.
For what values of r is the infinite geometric series ![]() convergent?
convergent?
The series is convergent if and only if ![]() For
For ![]() , the limit blows up to
, the limit blows up to ![]() . For
. For ![]() the limit alternates between
the limit alternates between ![]() For
For ![]() , the limit approaches
, the limit approaches ![]() . For
. For ![]() , the limit alternates between
, the limit alternates between ![]() . Since none of these limits approach 0, the series is divergent for
. Since none of these limits approach 0, the series is divergent for ![]() However, for the values
However, for the values ![]() , we can express
, we can express ![]() as a fraction
as a fraction ![]() , where
, where ![]() and
and ![]() . Therefore,
. Therefore,  since
since ![]() Therefore, the series is convergent for
Therefore, the series is convergent for ![]() .
.
If an infinite series converges, there may or may not be techniques for calculating the exact sum. For the case of the example, we will later show that the sum converges to ![]() for
for ![]() . Furthermore, if
. Furthermore, if ![]() and
and ![]() converge, then
converge, then ![]() converges, and
converges, and ![]() converges as well.
converges as well.
There are several tests to determine whether an infinite series of the form ![]() is convergent or divergent. For the case of an infinite series consisting only of non-negative terms, we have three tests at our disposal: the comparison test, the limit comparison test, and the integral test.
is convergent or divergent. For the case of an infinite series consisting only of non-negative terms, we have three tests at our disposal: the comparison test, the limit comparison test, and the integral test.
Let ![]() be a series with
be a series with ![]() for all k
for all k
(i) If ![]() is a convergent series with
is a convergent series with ![]() and
and ![]() for all k, then
for all k, then ![]() is also convergent.
is also convergent.
(ii) If ![]() is a divergent series with
is a divergent series with ![]() and
and ![]() for all k, then
for all k, then ![]() is also divergent.
is also divergent.
Limit comparison test:
Let ![]() and
and ![]() be series with
be series with ![]() and
and ![]() for all k
for all k
(i) If 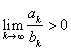 , then either both converge or both diverge.
, then either both converge or both diverge.
(ii) If 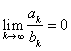 and
and ![]() converges, then
converges, then ![]() converges.
converges.
(iii) If 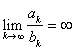 and
and ![]() diverges, then
diverges, then ![]() diverges.
diverges.
Integral test:
Let ![]() be a function that is continuous, positive, and decreasing for all
be a function that is continuous, positive, and decreasing for all ![]() . Then the infinite series
. Then the infinite series ![]()
(i) converges if the improper integral 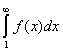 converges, and
converges, and
(ii) diverges if 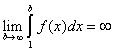 .
.
An example of each convergence test should help illustrate their power.
For the series ![]() ,
, ![]() , use the integral test to determine the values of
, use the integral test to determine the values of ![]() for which the series converges and diverges.
for which the series converges and diverges.
First, we note that ![]() is continuous, positive, and decreasing for
is continuous, positive, and decreasing for ![]() . For
. For ![]() , we find
, we find

Therefore, the series diverges for ![]() . For
. For ![]() ,
,
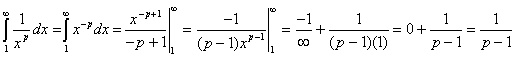
Therefore, the series converges for ![]() . Finally, for
. Finally, for ![]() ,
,
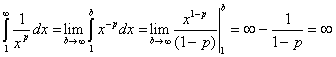
Therefore, the series diverges for ![]() . If we put it all together, we find that
. If we put it all together, we find that ![]() diverges for
diverges for ![]() and converges for
and converges for ![]() . The series for
. The series for ![]() is known as the harmonic series.
is known as the harmonic series.
Given the above conclusion that the harmonic series diverges, use the comparison test to determine whether ![]() converges or diverges.
converges or diverges.
For ![]() ,
, ![]() , so
, so ![]() . Since we know the harmonic series diverges, the comparison test tells us that
. Since we know the harmonic series diverges, the comparison test tells us that ![]() diverges as well.
diverges as well.
Solve the example using the limit comparison test, again using the harmonic series for comparison. Let ![]() and
and ![]() . We find,
. We find,
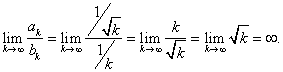
Therefore, part (iii) of the limit comparison test tells us that ![]() diverges.
diverges.
The study of infinite series is not restricted to positive terms. One common infinite series with both positive and negative terms is known as an alternating series. It has the form ![]() . The following theorem is a test of convergence specifically for the alternating series.
. The following theorem is a test of convergence specifically for the alternating series.
If the numbers ![]() alternate positive and negative, and if
alternate positive and negative, and if ![]() for all positive integers
for all positive integers ![]() , and
, and ![]() , then the alternating series
, then the alternating series ![]() is convergent.
is convergent.
Determine if the alternating series ![]() is convergent or divergent.
is convergent or divergent.
Note that this series has nearly the same terms as the harmonic series (which is divergent), but the signs alternate. ![]() and
and ![]() , and
, and ![]() for
for ![]() , so the first condition applies. We find
, so the first condition applies. We find ![]() , so this alternating series is convergent. The above series
, so this alternating series is convergent. The above series ![]() is convergent, but the harmonic series
is convergent, but the harmonic series ![]() is divergent. An infinite series like this is said to be conditionally convergent if
is divergent. An infinite series like this is said to be conditionally convergent if ![]() is convergent but
is convergent but ![]() is divergent. If both series are convergent, then
is divergent. If both series are convergent, then ![]() is said to be absolutely convergent. If a series is absolutely convergent, it is also convergent. With this understanding of absolute convergence, we introduce two new tests for absolute convergence: the ratio test and the root test.
is said to be absolutely convergent. If a series is absolutely convergent, it is also convergent. With this understanding of absolute convergence, we introduce two new tests for absolute convergence: the ratio test and the root test.
Let ![]() be an infinite series with
be an infinite series with ![]() for all k. Then
for all k. Then
(i) if 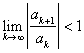 , the series is absolutely convergent (hence, convergent).
, the series is absolutely convergent (hence, convergent).
(ii) if 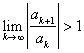 (including
(including ![]() ), the series is divergent.
), the series is divergent.
(iii) if 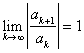 , the test is inconclusive.
, the test is inconclusive.
Root test:
Let ![]() be an infinite series with
be an infinite series with ![]() for all k. Then
for all k. Then
(i) if ![]() , the series is absolutely convergent (hence convergent).
, the series is absolutely convergent (hence convergent).
(ii) if ![]() , the series is divergent.
, the series is divergent.
(iii) if ![]() , the test is inconclusive.
, the test is inconclusive.
Using the ratio test, determine whether ![]() converges or diverges.
converges or diverges.
We find 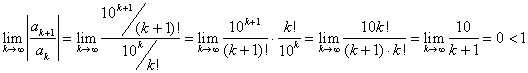 .
.
Therefore, the series is convergent.
Using the root test, determine whether  converges or diverges.
converges or diverges.
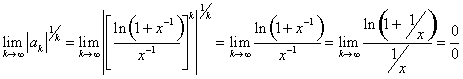 . Applying L’Hôpital’s rule,
. Applying L’Hôpital’s rule,
 . Therefore, the root test is inconclusive.
. Therefore, the root test is inconclusive.
We previously defined a power series in ![]() as a series of the form
as a series of the form
![]() . A power series in
. A power series in ![]() is of the form
is of the form
![]() where
where ![]() is a real number. However, we can easily convert this to the first power series by setting
is a real number. However, we can easily convert this to the first power series by setting ![]() and defining a power series in
and defining a power series in ![]() Therefore, we restrict our analysis to the first form of power series for the following section.
Therefore, we restrict our analysis to the first form of power series for the following section.
For the power series ![]() , we define the radius of convergence as a number
, we define the radius of convergence as a number ![]() such that s converges if
such that s converges if ![]() and diverges if
and diverges if ![]() . At
. At ![]() the series may either converge or diverge. If
the series may either converge or diverge. If ![]() converges only when
converges only when ![]() , then
, then![]() If
If ![]() converges for all real values of
converges for all real values of ![]() then
then ![]()
The set of values of ![]() for which
for which ![]() is convergent is known as the interval of convergence. If
is convergent is known as the interval of convergence. If ![]() is known, the interval of convergence can be determined. If
is known, the interval of convergence can be determined. If ![]() , the interval of convergence is 0. If
, the interval of convergence is 0. If ![]() the interval of convergence is
the interval of convergence is ![]() . Finally, if
. Finally, if ![]() it is necessary to check
it is necessary to check ![]() . Depending on the convergence or divergence at these two points, the interval of convergence is
. Depending on the convergence or divergence at these two points, the interval of convergence is ![]()
We can determine the radius of convergence by applying either the ratio test or root test to the ![]() portion of the series.
portion of the series.
For the power series 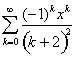 , what are the radius of convergence and interval of convergence?
, what are the radius of convergence and interval of convergence?
Apply the ratio test. 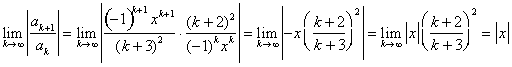
The ratio test tells us that if 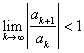 , then the series is convergent, and if
, then the series is convergent, and if  , then the test is inconclusive. So we know that if |x| < 1, then the series is convergent, and if |x| = 1, the series may or may not be convergent. We will need to check x = 1 and x= –1 individually. Either way,
, then the test is inconclusive. So we know that if |x| < 1, then the series is convergent, and if |x| = 1, the series may or may not be convergent. We will need to check x = 1 and x= –1 individually. Either way, ![]() .
.
Now we check ![]() and
and ![]() . At
. At ![]() , the series is
, the series is 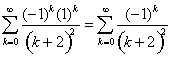 , which converges by the alternating series theorem. At
, which converges by the alternating series theorem. At ![]() , the series is
, the series is 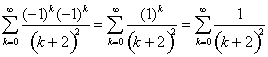 , which converges, as we saw in the example. Therefore, the interval of convergence is
, which converges, as we saw in the example. Therefore, the interval of convergence is ![]() .
.
If a power series has an interval of convergence, we can define a function ![]() to describe the power series for each
to describe the power series for each ![]() in that interval,
in that interval, ![]() . In some cases,
. In some cases, ![]() is a familiar function and is easy to derive. For example, we can derive
is a familiar function and is easy to derive. For example, we can derive ![]() for the simple geometric series
for the simple geometric series ![]() . In the example, we showed that
. In the example, we showed that ![]() exists in the interval of convergence of
exists in the interval of convergence of ![]() . We compute
. We compute ![]() . Since s is not infinite in the interval of convergence, we can subtract the second term from the first. Note that all terms except 1 are eliminated.
. Since s is not infinite in the interval of convergence, we can subtract the second term from the first. Note that all terms except 1 are eliminated.
So, ![]() . Therefore,
. Therefore, ![]() , or
, or ![]() for
for ![]() . With this, we can define other functions. For example,
. With this, we can define other functions. For example, ![]() , and
, and ![]() , where
, where ![]() still holds.
still holds.
Since a power series can be expressed as a function ![]() within its interval of convergence,
within its interval of convergence, ![]() exist within the same interval. For the differentiation and integration of power series, we perform the appropriate calculation—term by term. If the power series
exist within the same interval. For the differentiation and integration of power series, we perform the appropriate calculation—term by term. If the power series ![]() has a radius of convergence
has a radius of convergence ![]() , then for
, then for ![]() :
:
(i) ![]() is continuous.
is continuous.
(ii) ![]() exists.
exists.
(iii) ![]() exists.
exists.
Thus differentiating or integrating a power series forms a new series with the same radius of convergence. From this, we can derive other interesting functions expressed as infinite series.
From ![]() , for
, for ![]() , find the power series expression for
, find the power series expression for ![]() and
and ![]() for
for ![]() .
.
By differentiating, we find 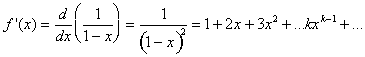
By integrating, we find 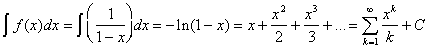 . By substituting
. By substituting ![]() , we find
, we find ![]() , or
, or ![]() . Therefore,
. Therefore, ![]() .
.
Prove that ![]()
First, we need to find the interval of convergence. By applying the ratio test, we find that 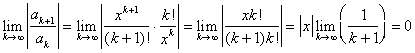 . Thus the radius of convergence is
. Thus the radius of convergence is ![]() , and the interval of convergence is
, and the interval of convergence is ![]() . Next, take the derivative of both sides of
. Next, take the derivative of both sides of ![]()
![]() , where we substituted
, where we substituted ![]() . Note that we find
. Note that we find ![]() . The solution for this differential equation is
. The solution for this differential equation is ![]() . At
. At ![]() ,
, ![]() , so
, so ![]() . This completes the proof.
. This completes the proof.
Since the function ![]() is continuous and differentiable within the same interval of convergence, it follows that higher order derivatives exist on the same interval. Since the series is infinite, the function
is continuous and differentiable within the same interval of convergence, it follows that higher order derivatives exist on the same interval. Since the series is infinite, the function ![]() is infinitely differentiable on the interval. Taking the first few derivatives of the power series, we find
is infinitely differentiable on the interval. Taking the first few derivatives of the power series, we find
![]() ,
,
![]() ,
,
![]() .
.
At this point, note the following patterns for ![]() .
.
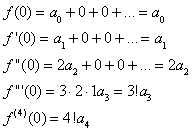
In general, we can define the coefficients ![]() as
as ![]() , and the power series in x can be rewritten as
, and the power series in x can be rewritten as
![]() .
.
The above series is known as the Maclaurin series. Generally, we can define the power series in ![]() ,
,
![]()
and take the same steps to show
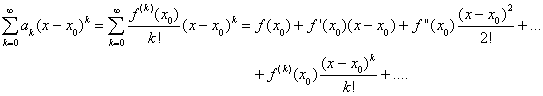
This series is known as the Taylor series of ![]() at
at ![]() . While the Maclaurin series has an interval of convergence
. While the Maclaurin series has an interval of convergence ![]() , the Taylor series has an interval of convergence
, the Taylor series has an interval of convergence ![]() . A series that is taken to the
. A series that is taken to the ![]() order rather than to
order rather than to ![]() is called an
is called an ![]() degree Taylor polynomial. In calculations, we typically use Taylor polynomials to attain a desired degree of accuracy.
degree Taylor polynomial. In calculations, we typically use Taylor polynomials to attain a desired degree of accuracy.
Suppose we define an ![]() degree Taylor polynomial as
degree Taylor polynomial as ![]() . We call the difference between the function
. We call the difference between the function ![]() and the Taylor polynomial the remainder term
and the Taylor polynomial the remainder term ![]() in the interval of convergence. Therefore,
in the interval of convergence. Therefore, ![]() . It can be shown that
. It can be shown that ![]() , where each
, where each ![]() is between
is between ![]() and
and ![]() .
.
Find the Maclaurin series expansion for ![]() .
.
Set ![]() . All higher order derivatives
. All higher order derivatives ![]() , so
, so ![]() . Therefore,
. Therefore,
![]()
Note that this was proven in the example to be true for all ![]() . Strictly speaking, this is not a formal proof that
. Strictly speaking, this is not a formal proof that ![]() has a series expansion. It simply shows that if
has a series expansion. It simply shows that if ![]() has a Maclaurin series expansion, then this series must be it.
has a Maclaurin series expansion, then this series must be it.
Find the Taylor series expansion for ![]() at
at ![]() .
.

The Taylor expansion is therefore
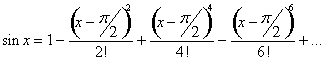
Approximate the value of ![]() using the first 6 terms of the Taylor expansion. Compute the value using a ten-digit calculator and determine why both answers are exactly the same.
using the first 6 terms of the Taylor expansion. Compute the value using a ten-digit calculator and determine why both answers are exactly the same.
In radians, ![]() . Using the above formula for
. Using the above formula for ![]() at
at ![]() ,
,
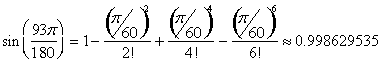
Using a ten-digit calculator, you should find the same value. The reason for this high degree of accuracy can be found in the remainder term. The error introduced by using the first six terms is ![]() , which is
, which is
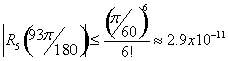
This shows that the above result should be accurate to ![]() decimal places, which is better than a ten-digit calculator.
decimal places, which is better than a ten-digit calculator.
Calculus (Ron Larson and Robert P. Hostetler): Houghton Mifflin, 2003.
Calculus Demystified: A Self-teaching Guide (Steven G. Kranz): McGraw-Hill, 2003.
Calculus Made Easy: Being a Very-Simplest Introduction to Those Beautiful Methods of Reckoning Which Are Generally Called by the Terrifying Names of the Differential Calculus (Silvanus Philips Thompson and Martin Gardner): St. Martin’s Press, 1998.
How to Ace Calculus: The Streetwise Guide and How to Ace the Rest of Calculus: The Streetwise Guide. (Colin Adams, et. al.): Henry Holt and Company, 1998.
The Complete Idiot’s Guide to Calculus (W. Michael Kelley): Alpha Books, 2002.
Don’t forget to test your knowledge with the Calculus Chapter Quiz;