Exponential Functions

What is an exponential function?

The basic form of an exponential function is

.

The variables are defined as:

• a is a constant,
• b is the base, and
• x is the exponent.

Exponential Growth

When b > 1, the function has exponential growth. An example of a growth function model is . This example is graphed below.

Exponential Decay

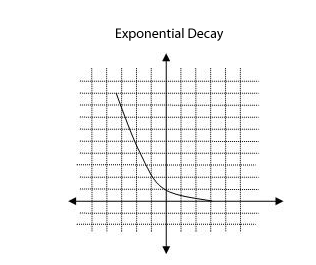
When 0 < b < 1, the function has exponential decay. An example of a decay function model is 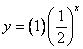. This example is graphed below.

The equation for compound interest is an excellent example of exponential growth. It is given by 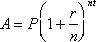, where P = principle, r = interest rate, n = compounding periods per year, t = time, and A = final amount.

How are logarithms used in exponential functions?

To solve exponential functions, we must first introduce the concept of logarithms. The definition of a logarithm is

.

Logarithms are very useful in solving exponential equations. Using logarithms, we now have a way to transfer the variable x out of the exponential position. This allows us to solve the equation.

Let’s try an example. Write the exponential equation  in logarithmic form.

Step 1: Notice the position of each number and the variable x in the exponential equation.

Step 2: Rewrite using the logarithmic equation.

How do we change the base of a logarithm?

When working with logarithms, it is often desirable to convert from one base to another. Frequently, we will want to convert to base 10. Many calculators only evaluate logarithms for base 10; therefore, we have to make the conversion before using the calculator to solve. The conversion, or change of base, formula is 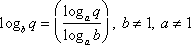, where b = the existing base, a = the new base, and q = a positive number. Let’s try an example. Convert  to base 10 and evaluate.

Step 1: In this problem, b = 4, a = 10, and q = 8.

Step 2: Use the change of base formula.

How do we solve exponential equations?

In order to solve an exponential equation, we must first isolate the variable located in the exponent. Once isolated, we can solve the equation.

For example, solve .

Step 1: Recognize that this is an exponential equation, with base 3. Convert to logarithmic form.

Step 2: Convert from base 3 to base 10.

Step 3: Solve for x.

Let’s try another example. Solve .

Step 1: Recognize that this is a logarithmic equation, with base 2. Convert to exponential form.

Step 2: Solve for x.

Review of New Vocabulary and Concepts

• Some conic sections, formed by the intersection of a single or double cone and a geometric plane, are:
  • circles,
  • parabolas, and
  • ellipses.
• Each conic has a standard form that determines the shape of the graph. The distance from the focus point to the vertex of a parabola is the same as the distance from the directrix to the vertex.
• Integer and fractional exponents follow the exact same rules for operations.
• Logarithms and the ability to convert between logarithmic and exponential form are essential in solving exponential equations.
• The change of base formula helps to convert between different bases when working with logarithms.

Further Reading in Algebra & Functions

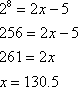
Algebra Demystified: A Self-teaching Guide (Rhonda Huettenmueller): McGraw-Hill, 2003.

College Algebra (Ron Larson and Robert P. Hostetler): Houghton Mifflin, 2003.

Practical Algebra: A Self-Teaching Guide (Peter H. Selby and Steve Slavin): John Wiley and Sons, 1991.

Schaum’s Outline of Intermediate Algebra (Ray Steege and Kerry Bailey): McGraw Hill, 1997.

Don’t forget to test your knowledge with the Algebra and Functions II Chapter Quiz;