Factoring Polynomials

Objective

Starting with a polynomial in standard form, you will study how to change a polynomial equation into a product of its individual terms.

Previously Covered:

• The different characteristics and classifications of polynomials, and how to determine the degree and number of terms in our classification.
• The operations of addition, subtraction, multiplication, and division with the goal of combining multiple polynomials into one final equation in standard form.

How are polynomials factored?

We will study the four methods of factoring, in addition to the preferred “trial and error” method:

1. factoring by using the distributive property;
2. factoring quadratic trinomials in the form  ;
3. factoring quadratic trinomials in the form  ; and
4. factoring in special cases.

First method—the distributive property

Polynomials can be factored by applying the distributive property by pulling out the common term of the polynomial. First find the greatest common factor (GCF).

For example, first find the GCF of  .

Each term can be written as a product of individual terms:

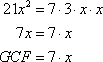
Remove the GCF from each term. Factoring out the GCF from each term the polynomial is factored as .

Question

Which choice shows the correct factorization of  by factoring out the GCF?

1. 
2. 
3. 
4. 

Reveal Answer

The correct answer is C. To find the GCF, expand each term.

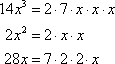
From this, we can see that the GCF is 2x, which can be factored out of each term in the original polynomial.

Second Method — Factoring quadratic trinomials in the form x² + bx + c

Multiplying two binomials using the FOIL method results in a polynomial in standard form.

To make the process easier, group the coefficients together as  for the linear term and rt for the constant term.

Comparing this to the standard form, we can see that the coefficient b on the linear term is equal to . The constant c is equal to rt. We now have two equations with two unknowns. Now find two numbers that, when added, result in b and when multiplied, result in c.

Trial and error becomes important in this step. Try different numbers, both positive and negative, that will satisfy these requirements.

Question

Which are the factors of the trinomial ?

1. 
2. 
3. 
4. 

Reveal Answer

The correct answer is D. In this equation, r and t must add to equal 5, and they must multiply to equal 6.

By trial and error (and inspection), or solving for each variable, we can conclude that r and t equal 3 and 2. Then, simply write the factors .

How do we know a trinomial is factored correctly?

If we use FOIL and multiply the two binomials (assuming the factors are correct), we will reproduce the original trinomial . If not, there was an error in the selection of r and t, and the process must be repeated until the correct numbers are found.

Third Method — Factoring quadratic trinomials in the form

Now there is a coefficient on the quadratic term equal to a and a third equation must be added to help find its value. With the addition of this coefficient, factoring the quadratic equation will produce two binomials in the form .

The equations become , , and . From here, the goal is to find m, n, r, and t. Remember that, as long as the trinomial is not too difficult, you can probably use trial and error to find the solution.

Question

Which is the correct factorization of ?

1. 
2. 
3. 
4. 

Reveal Answer

The correct answer is A. The following information is known:

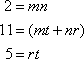
We see that m = 2, n = 1, and r = 1 and t = 5. In factored form,

.

Fourth method — Factoring special cases

Sometimes polynomials that initially seem complex can be factored easily by noticing special cases.

Difference of two squares : 

Perfect Square Trinomials : 

Question

Which shows the correct factorization of ?

1. 
2. 
3. 
4. 

Reveal Answer

The correct answer is B. Notice that the a-term and the b-term are perfect squares. We can write this trinomial as , which fits the perfect square trinomial formula. In factored form, this is .

Expand the binomial to check the answer.

Question

Which choice shows the correct factorization of ?

1. 
2. 
3. 
4. 

Reveal Answer

The correct answer is D. This is a difference of squares polynomial and can be written in the form . Apply the formula.

Use the FOIL method to check accuracy.

Why is factoring important?

Factoring is one method that lets us find the solution, or roots, of the polynomial. In graphical terms, this is the point or points where the graph crosses the x-axis and where the polynomial is equal to zero.

For example, three roots of a polynomial function are –2, 3, and 3. We can then write the following function in factored form:

Notice that  is equal to 0 if –2, 3, or 3 is substituted into this equation. Use the FOIL method to combine the first two binomials.

Use the distributive property to combine this trinomial and the third binomial.

If we draw the graph of , it is evident what roots mean.

On the x–y coordinate plane, the graph touches and reflects off of the x-axis at the point x = 3, and crosses the x-axis at x = -2. Because the graph reflects and does not cross the axis at x = 3, we have two identical roots at this point. Therefore, the roots for this polynomial are located at –2, 3, and 3.

Back to Top