 username@email.com
username@email.com
In this lesson, you will use coordinate systems to prove geometric theorems.
The basic tools of coordinate geometry are the distance and midpoint formulas and equations of lines, all of which were discussed in previous lessons.
We can put any parallelogram ABCD in a plane, such that A is the origin and B is a point on the positive x-axis, i.e. A=(0,0) and B=(r,0). Let C=(u,v) and D=(s,t). ![]() is parallel to
is parallel to ![]() , so the points C and D will have the same y-coordinate, i.e., v=t.
, so the points C and D will have the same y-coordinate, i.e., v=t.
Furthermore, since ![]() , u=r + s . So, in fact, C=(r + s, t).
, u=r + s . So, in fact, C=(r + s, t).
The diagonals are the line segments ![]() and
and ![]() . If P denotes the point of their intersection, we want to show that P is the midpoint of both the segments
. If P denotes the point of their intersection, we want to show that P is the midpoint of both the segments ![]() and
and ![]() . We can find P by finding the equations of the lines containing
. We can find P by finding the equations of the lines containing ![]() and
and ![]() .
.
The slope m1 of the line L1 containing ![]() is
is ![]() . Recall that (y – y1) = m(x – x1) is the equation of the line with slope m containing the point (x1, y1). Because L1 contains the origin, the equation of L2 is
. Recall that (y – y1) = m(x – x1) is the equation of the line with slope m containing the point (x1, y1). Because L1 contains the origin, the equation of L2 is ![]() . Similarly, the slope m2 of the line L2 containing BD is
. Similarly, the slope m2 of the line L2 containing BD is ![]() . Because L2 contains B = (r, 0), the equation of L2 is
. Because L2 contains B = (r, 0), the equation of L2 is ![]() .
.
To find x, set ![]() and solve for x.
and solve for x.
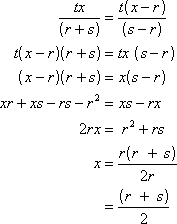
We can substitute x in either of the equations in order to find y.
![]()
So the coordinates of P are ![]() . If we apply the midpoint formula to A=(0,0) and C=(r+s, t), we get MAC=
. If we apply the midpoint formula to A=(0,0) and C=(r+s, t), we get MAC= ![]() = P. Similarly, if we apply it to B=(r, 0) and D=(s, t), we get MBD=
= P. Similarly, if we apply it to B=(r, 0) and D=(s, t), we get MBD= ![]() =P.
=P.
Since a rhombus is a parallelogram, we can use exactly the same set-up that we used in the previous proof.
We need to show that diagonals ![]() and
and ![]() are perpendicular using the equations of the lines L1 and L2 containing them.
are perpendicular using the equations of the lines L1 and L2 containing them.
What step must we show to finish the proof?
The correct answer is C . Two perpendicular lines have slopes that are negative reciprocals.
Geometry (Ray Jurgenson and Richard G. Brown): Houghton Mifflin, 1999.
Geometry for Dummies (Wendy Arnone): Wiley Publishing, Inc., 2001.
Schaum’s Outline of Geometry (Barnett Rich, et. al.): McGraw Hill, 1999.
Standard Deviants: Geometry DVD 2-Pack (Flavia Colonna and Rebecca Berg): Cerebellum Corporation, 2000.
Don’t forget to test your knowledge with the Geometry and Spatial Reasoning Chapter Quiz;