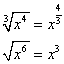username@email.com
username@email.com
In this lesson, you will study fractional exponents and the basic laws that govern how we add, subtract, multiply, and divide them. Also, we will discuss the radical as a popular type of fractional exponent.
We can only add or subtract like terms. The coefficients in front of the variable will combine, while the exponent will remain the same.
Which choice shows the correct simplification of ![]() ?
?
The correct choice is A. First, we must determine if the terms being added are like terms. Because each term has the same variable, with the same exponent, we know that these are like terms. We then must add the coefficients of each term, resulting in ![]() .
.
Which choice shows the correct simplification of ![]() ?
?
The correct choice is D. Again, we have to determine if we have like terms, and if so combine them. Any remaining terms stay separate. Since all terms have x as the variable, we look for terms with equivalent exponents. There are two pairs of like terms, so we combine the two pairs and get the following result.
![]()
![]()
We have combined all the like terms. Therefore, the correct choice is D.
When multiplying two or more terms with fractional exponents, the exponents are added together and the coefficients are multiplied. When dividing two or more terms, the difference of the exponents is found, and the coefficients are divided.
Which choice shows the correct simplification of ![]() ?
?
The correct choice is C. First, we multiply the coefficients together: (2)(4)(1) = 8. We then add the exponents.
![]()
Our final answer is ![]() .
.
Which choice shows the correct simplification of ![]() ?
?
|
Important Tidbit Remember that for negative exponents, |
The correct choice is B. We divide each term with the same variable, and subtract the corresponding exponents. The variable z is then multiplied.
![]()
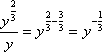
The terms combine, and result in ![]() . This answer can be rewritten with negative exponents as
. This answer can be rewritten with negative exponents as ![]() .
.
Earlier, we discussed radical symbols and how they can be converted into a variable raised to the one-half power. In other words, ![]() .
.
The variable x, when it stands alone or when it is beneath the radical, is raised to the first power, which accounts for the 1 in the numerator of the fractional exponent. The 2 in the denominator is derived from the fact that this is a square root.
Cube roots can also be converted to fractional exponents. In this case, ![]() .
.
We can continue this pattern to convert any variation of a radical raised to a power to a fractional exponent.
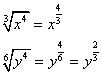
Let’s try an example. Multiply the radicals 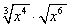 .
.
Step 1: Convert each radical to its equivalent fractional exponent.