username@email.com
username@email.com
In this lesson, you will study the properties of multiplication, division, addition, and subtraction for integer exponents. You will also study additional laws that come into play when solving expressions with a product of terms raised to a power, and the power of a power.
Only like terms can be added or subtracted. When combining like terms through either addition or subtraction, the coefficients in front of the variable will be combined, while the exponent will remain the same.
Which choice shows the correct simplification of 
?
The correct choice is A. First, we must decide if the terms being added are like terms. Because each term has the same variable, with the same exponent, we know that these are like terms. We then add the coefficients of each term, resulting in 
.
Which choice shows the correct simplification of 
?
The correct choice is D. Again, we have to determine if we have like terms, and if so, we must combine them. Any remaining terms stay separate. Since all of the terms have x as the variable, we must look for terms with equivalent exponents. There are three like terms and one separate term. 
,
and the separate term is 
.
Simplified, this is 
.
The product property states that when multiplying two or more terms with the same base, you should add the exponents. For example, 
. This is read, “y to the second power multiplied by y to the third power is equal to y to the fifth power.”
Which choice shows the correct multiplication of 
?
The correct choice is A. In this problem, both terms have the same base, x. Therefore, we add the exponents.
The power of a power property is used when an exponent is raised to a power. It states that when an exponent is raised to a power, we must multiply the exponent and the power. For example, 
. This is read, “x to the third power raised to the second power is equal to x to the sixth power.”
Which choice shows the correct simplification of 
?
The correct choice is A. The term 
is raised to the power of 3.Therefore, 3 is multiplied by 4 to get the final exponent, 12.
When a product of terms is raised to a power, the power is distributed to each term. For example, to simplify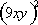 
the 2 is distributed to each term inside the parenthesis: 
.
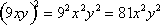Which choice shows the correct simplification of 
?
The correct choice is C. The term 
is a product of the terms 3, 
, and 
. The exponent 3 outside of the parentheses raises each individual term the power of 3. Therefore, 3 is distributed.
When dividing powers that have the same base, we find the difference of the exponents. For example,
.
Which choice shows the correct simplification of 
?
The correct choice is B. The numerator and denominator have the same base, therefore we find the difference of the exponents.
When the quotient is raised to a power, the power is distributed to each term in the numerator and denominator. For example,
.
Which choice shows the correct simplification of 
?
The correct choice is A. The power of 4 is distributed to each term in the numerator.
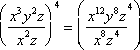
Then the quotient property can be used, and we can find the difference of exponents with the same bases.
.
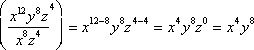For negative exponents, 
.
The zero property of exponents states that any number or variable raised to the power of zero is equal to one. This can be written 
, and 
.
Which choice shows the correct simplification of 
with positive exponents?
The correct choice is A. In this example, we can make use of the quotient property, and the rules for negative and zero exponents.
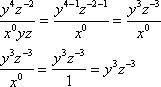
Finally, we can use the negative exponent property to write the equation with positive exponents.
