 username@email.com
username@email.com
In this lesson, we will investigate the relationship of ratio and similarity in convex polygons, focusing on similar triangles. We will also cover how to use ratios in order to solve problems relating to similarity and proportional segments.
From our experience with congruent triangles in the previous section, we know that congruence is an extremely strong condition. Congruence essentially means that two triangles are identical.
Similarity is a weaker concept. It means that two figures have the same shape, but are not necessarily the same size. In other words, one is a scaled version of the figure to which it is similar.
Two polygons are congruent if there is a correspondence between them such that every pair of corresponding sides is congruent and every pair of angles is congruent.
Two convex polygons are similar if there is a correspondence between their vertices such that the corresponding angles are congruent, and such that the ratios of the lengths of their corresponding sides are equal.
The polygons ABCD and EFGH shown above are similar, and we write polygon ABCD ~ polygon EFGH to denote the similarity.
In the similar quadrilaterals shown above, the ratio of the lengths of corresponding sides is 1:2, which can be directly verified. We can express this relationship using a series of equations called proportions.
![]()
A proportion is a sequence of equations stating that two or more ratios are equal.
Similarity, like congruence, is an equivalence relation. This means that similarity is reflexive, symmetric, and transitive. Any two of the ratios in a proportion are equal.
Use proportions to solve problems with similar figures.
Suppose that triangle ABC ~ triangle DBE as shown below. BD = 3, AD = 9, and DE = 6. Which choice shows the length of AC?
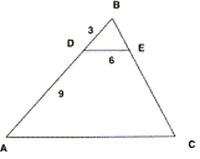
The correct answer is D . The proportion we would like to solve is ![]() . We are not given AB directly, but can determine its value using the information provided.
. We are not given AB directly, but can determine its value using the information provided.
![]()
Let x = AC.
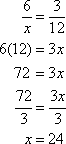
For the moment, we will focus on similar triangles because these are the simplest polygons. As in the case of congruent triangles, there are a number of situations in which we can give sufficient conditions for the similarity of two triangles.
Note that we could have called this the AAA postulate, but by a previous theorem on angles we know that if we have two congruent angles, the third is also congruent.
We will not prove the AA postulate here, but we will deduce an important corollary from it.
If a line parallel to one side of a triangle intersects the other two sides in distinct points, then it cuts off a triangle similar to the original triangle.
In our example, because DE is parallel to AC, we can view AB as transversal. We can then apply the theorem on transversal lines of corresponding angles, to conclude that angle BDE is congruent to angle BAC. Then we can apply the AA postulate to conclude that the triangles are similar since they share angle B.
This corollary is extremely useful in solving word problems that involve estimating distances. But before practicing with an exercise, here is another version of the corollary above that may also be useful in solving word problems.
If a line parallel to one side of a triangle intersects the other two sides in distinct points, then it cuts off line segments which are proportional to the sides. The following are the two analogues of the SAS and SSS congruence postulates.
Determine whether the pair of triangles is similar . If they are similar, which is the necessary postulate justifying this fact?
The correct answer is A . In the triangles, angle DCE and angle ACB are vertical angles, so they are congruent. It is also given that angle DEC and angle CAB are congruent. The triangles are therefore similar by AA similarity postulate.
Similar triangles have many applications in the real world. As is often the case with word problems, setting the problem up correctly is the hardest part. The following two exercises are a few of the many ways we can use similar triangles to estimate distances that may be impractical or impossible to measure.
A woman is running up a hill with a constant angle of incline. After running 10 miles, her altitude is 2 miles. Which choice shows her altitude after she has run 15 miles?
The correct answer is A. We can use the following diagram and the fact that the triangles are similar to solve the equation.
Set up a ratio based on the drawing, and then cross multiply to solve for x.
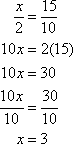
The map below shows a portion of New York City. If 21st, 22nd, and 23rd Streets are all parallel, how far is it along Broadway from 23rd Street to 21st Street?
The correct answer is D. Since the streets are parallel, the triangle formed by Broadway, 22nd, and 5th Avenue is similar to that formed by Broadway, 21st, and 5th Avenue. Denote the distance along Broadway from 23rd to 21st as x and set up a proportion.
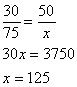
The last application of ratios we will cover in this section involves transversals and parallel lines .
If two transversals intersect three parallel lines, then the ratio of line segments cut off on one transversal is equal to the ratio of corresponding line segments cut off on the second transversal.
What is the length of the segment ![]() depicted in the figure below?
depicted in the figure below?
The correct answer is D . Using the postulate above, we know that ![]() . Substituting the information given in the figure, we get that AC = 5 + 7 = 12, and
. Substituting the information given in the figure, we get that AC = 5 + 7 = 12, and ![]() , where x = DE . Solve this equation.
, where x = DE . Solve this equation.
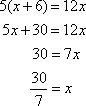
The ratio could also be setup as:
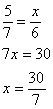
Therefore, if we know that DE = 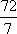 , then DF = DE + 6, or
, then DF = DE + 6, or 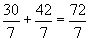 .
.