username@email.com
username@email.com
In this lesson, you will study how to simplify, add, subtract, multiply, and divide rational polynomials.
; in the form 
; and in special cases, such as the difference of two squares and perfect square trinomials.A rational polynomials a polynomial with rational coefficients. The word rational here is connected to the term ratio, because a rational number can be expressed as a ratio of integers. Likewise, a rational function or a rational polynomial can be expressed as a ratio of two polynomials.
For example:
The numerator consists of a linear equation, and the denominator is a quadratic.
How do we simplify rational polynomials?
Simplifying rational polynomials is directly related to the methods in the previous section—factoring and finding the greatest common factors of polynomials. Before a rational polynomial can be completely simplified, the GCF has to be extracted from the polynomial (if one exists) and the resulting polynomial has to be factored (if possible).
For example, simplify the rational polynomial 
.
First, we must determine whether a GCF exists and, if so, factor it out of the polynomial. In this example, the denominator has a GCF = 3. Rewrite the ratio, factoring 3 out of the denominator.
Now try factoring each quadratic in the numerator and
denominator to see if any common terms will cancel.
The linear term 
is common in both numerator and denominator, so it can be cancelled or divided out. The simplified final answer is 
.
Which shows the correct simplification of the rational polynomial 
?
The correct answer is D. The first step is to see if a GCF exists in either polynomial. In this problem there is not a GCF, so we proceed to factor each quadratic. Doing so results in the ratio 
. The next step is to cancel any common terms. In this case the linear term 
is present in both the numerator and denominator, so it can be canceled or divided out. The final simplified answer is 
.
Adding and Subtracting Rational Polynomials
The process of adding and subtracting rational polynomials follows the procedure for combining simple fractions. The difference is that the common denominator is a polynomial instead of a number. Once a common denominator is established, the numerators can be added or subtracted.
For example, add the two rational polynomials 
by first finding the common denominator, in this case, 6x. Multiply the first polynomial by 
and the second polynomial by 
to get a common denominator. Then add the numerators and simplify. You will not change the value of the expression when you find a common denominator since you are multiplying each part by one.
Which of the following correctly combines the two rational polynomials 
?
The correct answer is A. To subtract, use the same method as you would when adding. First, establish a common denominator. For this problem, the common denominator is 10x. We then multiply each numerator by the opposite denominator to “balance” each ratio, giving us the following equivalent expression:
Multiplying Rational Polynomials
Once again, multiplying rational polynomials follows the same rules as multiplying two fractions—numerators are multiplied together, and denominators are multiplied together.
For example:
The polynomial 2x (which is actually 
) is multiplied by the numerator.
After multiplying, check for any common terms in the numerator and denominator to further simplify the ratio. To do this, factor the denominator and see if a common term exists.
can be canceled or divided out, leaving 
.
After performing the operation, remember to simplify by canceling any common GCF terms or common polynomial expressions.
Division consists of simply multiplying by the reciprocal, or, in common terms, “flipping” the second ratio, and changing the operation from division to multiplication.
For example:
This is the exact procedure for rational polynomial division.
For example, simplify the rational expression 
.
The first step is to multiply by the reciprocal of the second polynomial.
Notice that there is a quadratic is in the numerator of the second ratio. Factor this, with the hope of finding a common term to cancel.
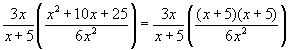
The common term 
cancels from the numerator and denominator. 3x will also cancel out of the numerator and denominator leaving 
.
If there are variables in the denominator after simplification, then we can expect to find asymptotes as part of our graph since there will be values for the denominator equal to zero. For example, draw the graph of 
.
