What is a dot product?
A dot product of two vectors,  and
and 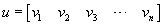 , is denoted
, is denoted 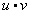 and is defined:
and is defined: 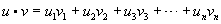
In two dimensions, a vector can be graphed onto an xy-coordinate plane.

The graph shows two vectors u = [2 3] and v = [4 1]. The blue vector is described as u – v.
By the Law of Cosines, 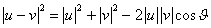 , where
, where 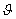 is the interior angle between u and v.
is the interior angle between u and v.
Simplifying:
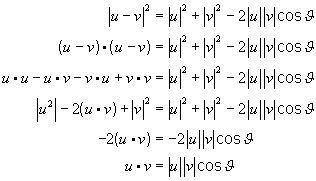
Thus, the dot product is the product of the lengths of the two vectors and the cosine of the angle between the vectors. More helpfully, 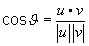 , provided u and v are non-zero vectors.
, provided u and v are non-zero vectors.
For example, to find the angle between the two vectors u = [2 3] and v = [4 1],
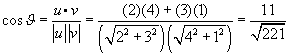
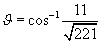
Question
If the dot product of two non-zero vectors is 0, then what must be true about the vectors?
- The vectors are perpendicular.
- The vectors are equal to each other.
- One vector is a scalar multiple of the other.
- The vectors do not exist.
Reveal Answer
The correct choice is A. If 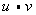 = 0, and the vectors are non-zero, then
= 0, and the vectors are non-zero, then 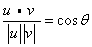 . When the cosine is 0, the angle must be 90°.
. When the cosine is 0, the angle must be 90°.
What are Cross Products?
We define the cross product only for three-dimensional vectors.
Let u = 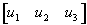 , and v =
, and v = 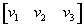 .
.
And let i, j, and k be the unit vectors [1 0 0], [0 1 0], and [0 0 1] respectively.
The cross product 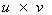 is the determinant
is the determinant 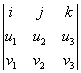 .
.
Important Tidbit
The cross product is a vector. It is perpendicular to the plane on which the original two vectors lie. So the cross product u × v is a vector perpendicular to the plane in which both u and v lie.
Question
What is the cross product of u = [4 –2 3] and v = [–1 2 1]?
- –5
- –48
- 3i + 0j + 4k
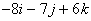
Reveal Answer
The correct choice is D. The cross product yields the vector 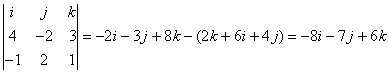 .
.
Does the cross product have a special geometric interpretation?
- The length of the cross product of
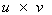 is the area of a parallelogram that has sides of u and v.
is the area of a parallelogram that has sides of u and v.
- The length of the cross product of
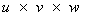 is the volume of the parallelepiped created by u, v, and w.
is the volume of the parallelepiped created by u, v, and w.
Review of New Vocabulary and Concepts
- The number of solutions of a system of linear equations can be determined by graphing the system.
- The number of solutions of a system of linear equations is also evident by the symbolic manipulations of the equations.
- A three-variable linear system with one solution can be graphed as three planes meeting at exactly one point.
- A three-variable linear system with no solution can be graphed as three planes that never coincide at the same time.
- A three-variable linear system with an infinite number of solutions can be graphed as two or three planes that meet at a line.
- A two-variable linear system with one solution can be graphed as two lines that meet at exactly one point.
- A two-variable linear system with no solution can be graphed as two parallel lines that, of course, never cross.
- A two-variable linear system with an infinite number of solutions is graphed as one line because both equations describe the same line.
- Determinants can be used in a number of geometric applications.
- A dot product between two vectors produces a scalar.
- A cross product between two vectors produces a vector.
- Using the Law of Cosines, we developed a relation using the dot product and the length of the
two vectors to determine the angle between two vectors.
Further Reading in Linear Algebra
Linear Algebra and its Applications (David C. Lay): Pearson Addison Wesley, 2002.
3,000 Solved Linear Algebra Problems (Seymour Lipschutz): McGraw Hill, 1989.
Don’t forget to test your knowledge with the Measurement and Linear Algebra Chapter Quiz;
 username@email.com
username@email.com
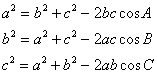 .
.![]() and
and ![]() , is denoted
, is denoted ![]() and is defined:
and is defined: ![]()
![]() , where
, where ![]() is the interior angle between u and v.
is the interior angle between u and v.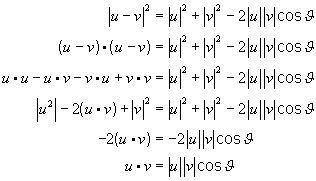
![]() , provided u and v are non-zero vectors.
, provided u and v are non-zero vectors.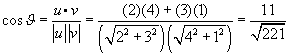
![]()
![]() = 0, and the vectors are non-zero, then
= 0, and the vectors are non-zero, then ![]() . When the cosine is 0, the angle must be 90°.
. When the cosine is 0, the angle must be 90°.![]() , and v =
, and v = ![]() .
.![]() is the determinant
is the determinant 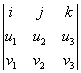 .
.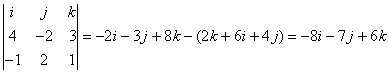 .
.