 username@email.com
username@email.com
In this lesson, we will prove the Pythagorean Theorem and its converse, and we will prove the formulas for special right triangles that were covered in a previous section.
One of the pillars of geometry is a well-known theorem created by the Greek mathematician Pythagoras:
For any right triangle with legs a and b and hypotenuse c, the following relationship is satisfied: a2 + b2 = c2
In other words, the square of the hypotenuse is equal to the sum of the squares of the legs in any right triangle.
The Pythagorean Theorem is a fundamental geometric principle that shows up in geometry and trigonometry. We will use it in a later section to derive the equation of a circle.
There is more than one way to prove the Pythagorean Theorem, but we will only cover only one approach here.
Suppose we are given any right triangle with side lengths a, b, and c, where c is the length of the hypotenuse.
Step 1: If we take a square with side length a + b, we can draw four triangles inside the square with legs a and b as shown below.
Step 2: These four triangles are congruent by the SAS postulate. Therefore, they all have a hypotenuse of length c.
Step 3: The quadrilateral formed by the four sides of length c is a square . This follows from the fact that the angles labeled 1 and 2 add up to 90 ° , and that one angle of the quadrilateral is the supplement of the angles 1 and 2.
Step 4: The area of the larger square is equal to the area of the four congruent triangles plus the area of the smaller square.
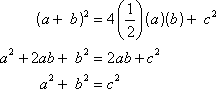
We can also prove two theorems from the previous section on special right triangles using the Pythagorean Theorem.
In a 30-60-90 triangle, the length of the hypotenuse is twice the length of the shorter leg and the length of the longer leg is ![]() times the shorter leg.
times the shorter leg.
If we reflect a 30-60-90 triangle across its longer side, we obtain an equilateral triangle. Label the sides a, b, and c. Thus ![]() , or equivalently, c = 2b. Find c by using the Pythagorean Theorem:
, or equivalently, c = 2b. Find c by using the Pythagorean Theorem:
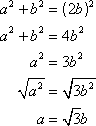
In a 45-45-90 triangle, the length of the hypotenuse is ![]() times the shorter leg. Label the length of the two congruent sides a and the hypotenuse c. Then by the Pythagorean Theorem,
times the shorter leg. Label the length of the two congruent sides a and the hypotenuse c. Then by the Pythagorean Theorem,
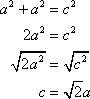
If a rectangle has a diagonal of length 13 and a side of length 5, what is the length of the longer side?
The correct answer is C . By the Pythagorean Theorem, we have ![]() , where x is the length of the longer side.
, where x is the length of the longer side.
Simplify to find the value of x: ![]() .
.
The converse of the Pythagorean Theorem is as follows:
If the sum of the squares of the lengths of two sides of a triangle is equal to the square of the length of the third side, then the triangle is a right triangle.
To prove the converse, we need to show that one of the angles is a right angle . If we show congruence between the given triangle and a right triangle, then we will have proved the converse .
Suppose we are given a triangle angle ABC with sides a, b, and c satisfying a2 + b2 = c2.
Step 1: Take a right triangle angle DEF with legs of length a and b and hypotenuse d.
Step 2: triangle DEF is a right triangle, so a2 + b 2 = d 2 by the Pythagorean Theorem.
Step 3: By the SSS postulate, triangle ABC and triangle DEF are congruent. So angle ABC is a right triangle.
In a cube with side length s, what is the length of a diagonal d connecting opposite faces as shown in the figure below?
The correct answer is B . The first step in finding the length of d is finding the length l of a diagonal on a face (see the figure below). d is the hypotenuse of a right triangle with legs l and s . By the Pythagorean Theorem, ![]() , or
, or ![]() . A second application of the Pythagorean Theorem gives
. A second application of the Pythagorean Theorem gives ![]() .
.