 username@email.com
username@email.com
In this lesson, you will study some of these basic properties of transversals and triangles in this section and give sufficient conditions for the congruence of triangles. You will also prove some of these theorems as simple corollaries of others.
• A polygon is the union of the n segments P1, P2, P2, P3, . . . P3, P1 such that P1, P2 . . . Pn is a sequence of n distinct points in the plane, with ![]() satisfying the following properties:
satisfying the following properties:
• A triangle is a polygon in which n = 3.
A transversal to two lines in the plane is a line that intersects them in two different points.
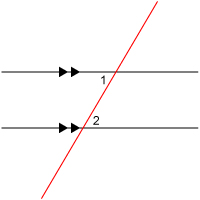
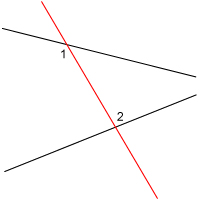
The lines cut by the transversal are not necessarily parallel, as shown in the first picture above. In both cases, the angles labeled by 1 and 2 are referred to as alternate interior angles. Note that there are two pairs of alternate interior angles.
The most important theorems involving transversals are in the case of parallel lines:
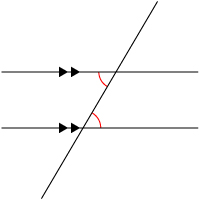
Which is the measure of the angle denoted by x in the figure below?
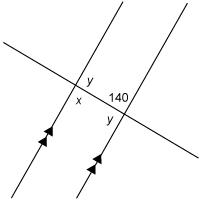
The correct answer is D. The existence of the pair of congruent alternate interior angles (the pair with measure y-span >) tells us that the lines L 1 and L 2 are parallel. The fact that the lines are parallel allows us to use the second theorem to deduce that the other pair of alternate interior angles is congruent, so x = 140.
In fact, the example above is a special case of a corollary of the two theorems on transversals.
The proof of this is sketched in the explanation of the correct answer to the example question above. If we replace the number 140 with an arbitrary angle measure of x and follow the same reasoning, then we have a proof.
The answer to this question is actually a postulate created by Euclid, the famous geometer.
Existence and Uniqueness of Parallel Lines: Let L be any line and P be a point not on L. Then there is only one line containing P parallel to L.
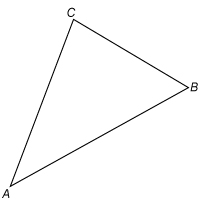
We can label any triangle by labeling its vertices. The triangle ABC is shown below.
The most basic property concerning the angles of the triangle is given by the following theorem.
The Triangle Angle Sum Theorem:The sum of the interior angles of a triangle is 180°.
What is the measure of angle A in the picture below?
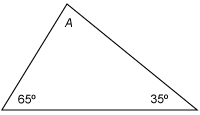
The correct answer is B. We find the measure of angle A, which we denote by the variable x and solving the equation ![]() .
.
As is often the case in geometric proofs, it boils down to thinking about the right picture. If we consider the first picture below, then we are in an ideal position to use the theorem on transversals. But, as in the case with any mathematical proof, we need to justify each step and our picture.
Step 1 For any triangle span >ABC, we can label the measure of the three interior angles by the variables x, y, and z.
Step 2 By the theorem on the existence of parallel lines in the previous subsection, we know that there exists a line parallel to ![]() containing C. This justifies the picture drawn below.
containing C. This justifies the picture drawn below.
Step 3 Apply the transversal theorem involving alternate interior angles to the angles yspan > and z.
Step 4 Thus, the angles x, y, and z are supplementary, ![]() .
.
Just by drawing the right picture and using one other theorem, we were able to show that the angle sum of the triangle is 180°.
Now use the Triangle Angle Sum Formula to prove the following theorem:
If two angles of one triangle are congruent to two angles of another triangle, then the remaining angles are congruent.
Suppose we denote the measure of the first pair of angles by x and the second by y. Then ![]() and
and ![]() by the Triangle Angle Sum Theorem. So w = span > z, which shows that the remaining angles are congruent.
by the Triangle Angle Sum Theorem. So w = span > z, which shows that the remaining angles are congruent.
We compare triangles by comparing their sides and angles. Angles are congruent if they have the same angular measure. Sides are congruent if they have the same length. We can extend the idea of congruence to triangles as follows.
A correspondence between two triangles is a match-up between its vertices. For example, in the two triangles shown below, if the vertex A corresponds to D and the vertex B corresponds to E and the vertex C corresponds to F, then the triangle ABC corresponds to the triangle DEF. We write ABC ![]() DEF.
DEF.
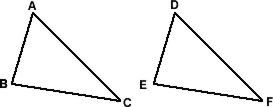
The ordering is very important. Any correspondence between triangles automatically gives us a correspondence between its sides and its angles. This will allow us to define congruent triangles.
A correspondence ABC ![]() DEF between two triangles is called congruence if every pair of corresponding sides is congruent and every pair of angles is congruent. If such congruence exists, we denote this relationship by
DEF between two triangles is called congruence if every pair of corresponding sides is congruent and every pair of angles is congruent. If such congruence exists, we denote this relationship by ![]() ABC
ABC ![]()
![]() DEF. In fact, congruence between two triangles is actually six relations: three angle congruences and three side congruences.
DEF. In fact, congruence between two triangles is actually six relations: three angle congruences and three side congruences.

When comparing triangles, indicate congruence of sides and angles by marking the figures as shown below.
In the example above, we showed that if two pairs of corresponding angles are congruent then the third pair of corresponding angles is congruent. If we relax some of these six conditions, however, is the congruence of the triangles still implied? There are three well-known situations in which this is the case. These are known as the SSS postulate, the SAS postulate, and the ASA postulate.
A side of a triangle is said to be included by the angles the vertices of which are the endpoints of the side . In the picture below the side ![]() is included by angle F and angle G.
is included by angle F and angle G.
An angle of a triangle is said to be included by the sides of the triangle which make up that angle . In the picture above, angle H is included by the sides ![]() and
and ![]() .
.
If three sides of one triangle are congruent to three sides of another triangle, then the two triangles are congruent.
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the two triangles are congruent.
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
The correct answer is C . There is no SSA Postulate as shown by the pair of triangles below.
Although it is not as well known as its siblings, there is one more postulate we can use to show that two triangles are congruent.
If two angles and a non-included side of one triangle are congruent to two angles and the non-included side of another triangle, then the two triangles are congruent.