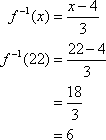username@email.com
username@email.com
In this lesson, you will cover the definitions and uses of composite and inverse functions.
The fact that a variable can be a function of a function leads us to the concept of composite functions. Suppose, for example, that Doug is selling magazines from door to door. He earns a 10% commission on every subscription he sells. By subscribing for a year, the customer saves 50% off the retail price. If a customer subscribes to a magazine that usually sells for $60 per year, what will Doug’s commission be?
To find out, we use a chain of functions. Doug’s commission is a function of the subscription selling price, which in turn is a function of the retail price. Let Doug’s commission equal DC, let S equal the subscription price, and R equal the retail price.
.
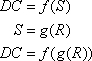
In the example, R = $60. Doug’s commission = (ƒο g) (R). Solve for DC.
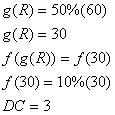
Let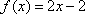 
and 
. Which choice shows 
?
The correct answer is B. You know that 
. To find , substitute 
for x in ƒ(x).
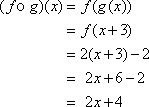
Let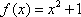 
and 
. Which choice shows 
?
The correct answer is D. First, find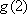 
.
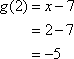
The substitute –5 for x in 
.
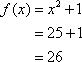
You know that a relation is a set of ordered pairs. If we exchange the domain for the range of the relation, we create a new relation called the inverse relation. If, when we create the inverse relation of a function, that inverse relation is also a function, it is called an inverse function. We notate the inverse function for 
with 
.
Recall the earlier example of children in preschool and their ages.
| Child’s name | Age |
|---|---|
| Mary | 3 |
| Ashley | 4 |
| Brian | 2 |
| Charlie | 3 |
| Katie | 3.5 |
As long as the children constituted the domain and their ages constituted the range, the relation was a function. Mapping the ordered pairs of the children and their ages in the opposite direction, however, did not produce a function. Both Mary and Charlie were paired with 3. If three was a member of the domain rather than the range, it would have two members of the range paired with it. Therefore, interchanging the domain and the range would result in another relation, but not a function. All relations have inverse relations. Not all functions, however, have inverse functions.
The ordered pairs of an inverse relation can be found by interchanging the x- and y-values in the pairs. The inverse relation of {(1, 2) (3, 4) (5, 6) (7, 8)} is {(2, 1) (4, 3) (6, 5) (8, 7)}. Graphically, a relation and its inverse will produce a reflection across the line y = x.
Find the inverse of a function that is an equation by exchanging the variables.
For example, let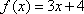 
. Substitute y for f(x), exchange variables, and solve for y.
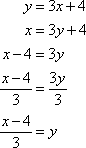
If we have found the inverse, it will undo the original function. That is, if ƒ(x) = y, then ƒ–1(y) = x. Use 6 to check our work.
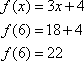
If the functions are inverses, then ƒ –1(22) should equal 6.
