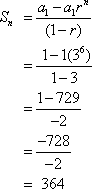username@email.com
username@email.com
In this section, you will study the definitions of geometric and arithmetic sequences and the formulas for finding terms and summations for arithmetic and geometric sequences.
A sequence is an ordered set of numbers that are related mathematically. It is a function in which the domain is the set of integers or the set of natural numbers. We use the letter n to stand for the independent variable. For example:
![]()
If we restrict the domain to the set of natural numbers, then we can write the equation in functional notation.
![]()
Using our function, we see
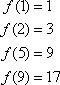
The sequence of numbers is 1, 3, 5, 7, . . . . for ![]() . Each value in a sequence is called a term.
. Each value in a sequence is called a term.
In sequence notation, the first term is denoted a1. The second term is a2, and so on through an for the nth term. Positive integers are represented by n. We call the nth term the general term.
If a sequence stops at a given term, it is a finite sequence. A sequence like the one above, that continues indefinitely, is called an infinite sequence. An infinite sequence is written using an ellipsis ( . . . ) to show that it does not end.
Rewriting our sequence in sequence notation gives
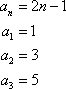
You can get any term in the sequence by adding two to the previous term. A sequence such as this, in which a constant is added to the previous term to get the next term, is called an arithmetic sequence. The constant is called the common difference.
If you know the initial term and the common difference, you can generate a rule for finding any term by operating on the previous term. This rule would be called a recursive formula. You must know the previous terms to find a particular term in a sequence. The recursive formula for the sequence we have been working with is
![]()
This recursive formula enables us to write an explicit formula. An explicit formula enables us to find the
value of any term without knowing the value of the previous term. The explicit formula for our sequence is ![]() where d is the common difference.
where d is the common difference.
Find the 11th term in the sequence.
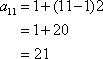
The sum of the terms in an arithmetic sequence is called an arithmetic series. A partial sum of a series adds all the terms prior to the selected term. A partial sum can be found even if a sequence is infinite. For example,
arithmetic sequence: 1, 3, 5, 7, . . .
arithmetic series: 1 + 3 + 5 + 7 + . . .
Here are a few partial sums for the series ![]()
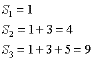
Use the Greek letter sigma, Σ, to write a series in series notation. For example, to show that we want to find the 8th partial sum of the series we have been working with, use ![]() . The formula below means the sum from n = 1 to 8 of the terms 2n – 1.
. The formula below means the sum from n = 1 to 8 of the terms 2n – 1.
![]()
You can also use the following formula to find the partial sum of an arithmetic sequence:
![]()
Again using the series we have been working with, where n = 8, a1 = (2 × 1 − 1) = 1 and d, the common difference, equals 2 , we get:
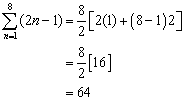
Which is the correct simplification of ![]() ?
?
The correct answer is A. In expanded notation, ![]() .
.
Recall that in an arithmetic sequence, the difference between any two consecutive terms is a constant called the common difference. In a geometric sequence, or geometric progression, there is a common ratio between any two consecutive terms. In other words, the division of any term by the term just previous to it results in the same number. This ratio is called the common ratio.
For example, given the sequence 1, 3, 9, 27, . . .
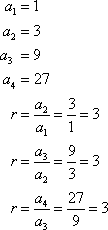
A sequence a1, a2, a3, . . . an is a geometric sequence if for all n > 1, ![]() , where r is the common ratio.
, where r is the common ratio.
Using this formula for r, we get a recursive formula for the sequence.
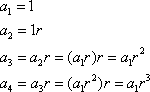
Note that each time we replaced the new term with the preceding term times r. We can continue this process until we get ![]() . This is the formula to find the nth term, also known as the common term, of a geometric sequence. You can find the common term if you know the first term and the common ratio.
. This is the formula to find the nth term, also known as the common term, of a geometric sequence. You can find the common term if you know the first term and the common ratio.
Which is the sixth term of the geometric sequence 1, 2, 4, 8, . . . ?
The correct answer is C. To solve, use the formula 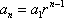 .
.
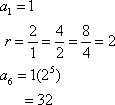
The summation of the terms in a geometric sequence is a geometric series. A finite geometric series is the summation of the terms in a finite geometric sequence.
For example, if r ≠ 1 is the common ratio, then 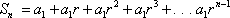
Multiply both sides of the equation by r.
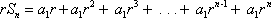
Subtract the two equations.
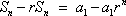
Factor the left side.
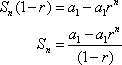
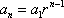 , and therefore
, and therefore 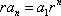 .
.
Finally, replace 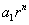 with
with 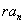 in the formula.
in the formula.
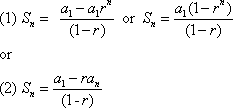
You can use formula (1) to find the sum of a geometric series when you know the first term and the common ratio. When you know the first term, the last term, and the common ratio, you can use formula (2), which does not require raising the common ratio to powers.
Which choice shows the sum of the first 6 terms in the sequence 1, 3, 9, 27, . . . ?
The correct answer is D. We do not know the 6th term, so we use formula (1).