 username@email.com
username@email.com
In this lesson, you will focus on determining the surface area and volume of three-dimensional figures. You will also explore how changing dimensions of a figure changes the size of the surface area and the volume.
To determine the surface area of a figure, first think about disassembling the figure into separate faces. For instance, think about a right rectangular parallelepiped with dimensions of 6 centimeters by 8 centimeters by 20 centimeters.
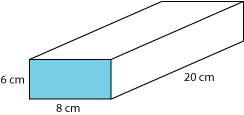
There are six faces.

The surface area of the figure is the sum of the areas of the six faces.
A = 2(6)(8) + 2(6)(20) + 2(8)(20) = 656
square centimeters
What is the surface area of a cylinder that is 15 feet in diameter and 8 feet high?
The correct choice is D. The cylinder can be deconstructed into three faces- two circles and one rectangle.
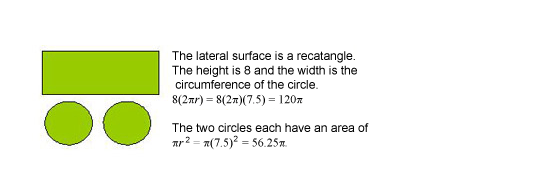
The surface area is the sum of the three faces, ![]() .
.
There are a number of volume formulas. In this section, we will explore two basic categories of volume formulas: non-pointed and pointed figures.
First, let’s review some formulas for non-pointed solids:
These first three formulas refer to non-pointed figures. Notice that each figure in this category has a volume that can be calculated by multiplying the area of its base by its height.
A rectangular solid is also called a rectangular parallelepiped.
A solid with trapezoidal bases and rectangular sides is also called a trapezoidal parallelepiped.
Next, let’s consider solids that are pointed at the top.
These three formulas refer to pointed figures. Notice that the volume of each pointed figure is ![]() of the area of the base multiplied by the height.
of the area of the base multiplied by the height.
To find the volume of a non-pointed solid, multiply the area of the base by the height of the solid, measured at a right angle to the base.
To find the volume of a pointed solid, multiply the area of the base by the height of the solid, measured at a right angle to the base, and divide by 3.
The solid below has a right triangular base. What is the volume?
The correct choice is A. The volume is the area of the triangular base multiplied by the height of the solid: ![]() . Volume is always measured in cubic units.
. Volume is always measured in cubic units.
What is the approximate surface area of the solid in the question above?
The correct choice is D.Surface area is measured in square units. The solid has 5 faces. The bases are two isosceles right triangles, each with 2 sides of length 4 inches and a third side of length ![]() . There are two 3 by 4 rectangles and one rectangle that is 3 by
. There are two 3 by 4 rectangles and one rectangle that is 3 by ![]() .
.
The total surface area is
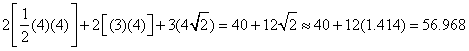 .
.
Take the figure below, for example. The orange rectangle is 4 by 6 and has an area of 24 square units.
The yellow rectangle has the dimensions of the orange rectangle multiplied by a factor of three, which results in dimensions of 12 by 18. The area of this rectangle is 216 square units, which is the area of the orange rectangle multiplied by the square of the factor of three, or nine.
![]()
The blue rectangle has the dimensions of the orange rectangle multiplied by a factor of one-half, which results in dimensions of 2 by 3. The area is 6 square units, which is the area of the orange rectangle multiplied by the square of the factor of one-half, or one-fourth.

Let’s say that these rectangles are actually solids. If the orange solid were 4 by 6 by 2, it would have a volume of 48 cubic units.
If the dimensions of the yellow rectangular solid differ from the dimensions of the orange solid by a factor of three, its dimensions would be 12 by 18 by 6. The volume of the yellow rectangular solid would be 1,296 cubic units, which is the volume of the orange rectangular solid multiplied by the cube of the factor of three.
![]()
If the dimensions of the blue rectangular solid differ from the dimensions of the orange solid by a factor of one half, the dimensions would be 2 by 3 by 1. The volume of the blue rectangular solid would be 6 cubic units, which is the volume of the orange rectangular solid multiplied by the cube of the factor of one-half.

A statue of a horse has a volume of 12 cubic meters. The artist’s model had dimensions of one-tenth of the final statue. What was the volume of the artist’s model?
The correct choice is A. The dimensions of the model were one-tenth the dimensions of the statue, so the volume of the model would be  of the original.
of the original.
![]()
How many square inches are in a square foot?
The correct choice is D. A square foot is 12 inches by 12 inches; it has an area of 144 square inches.
A copy machine increases the area of a figure to 200% of the original. If the original height of the figure is 6 units, what is the height of the final figure?
The correct choice is B. The area was doubled, so the lengths of the sides must have been increased by a factor of the square root of two.