 username@email.com
username@email.com
In this lesson, you will study how to solve equations and inequalities containing absolute values.
The absolute value of a number x is its distance from zero on a number line. Absolute value is a non-negative number that is concerned only with distance from zero, not the direction one must move on the number line to find the number. The absolute value of x is written │x│.
If x is any real number, then
![]() = x if x > 0
= x if x > 0
![]() = 0 if x = 0
= 0 if x = 0
![]() = x if x < 0
= x if x < 0
Therefore,![]() = a if and only if x = a or x = –a.
= a if and only if x = a or x = –a.
Remember that the negative of a negative number is a positive. Absolute value is always positive.
What is the value of x in the equation ![]() = 5?
= 5?
The correct answer is C. Using the theorem, we see that x = 5, or x = –5. The solution set is {x│ x = 5 and x = – 5}.
What is the value of x in the equation ![]() = –6?
= –6?
The correct answer is D. There is no solution to this problem because absolute value cannot be negative.
To solve an equation using more than one term and absolute value, take what is inside the absolute value sign and set it equal to a constant and the negative of the constant.
For example, solve the equation │4x + 4│ = 44. First, set 4x + 4 equal to 44 and solve.
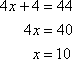
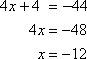
The distance between two values, a and b, is given by │b – a│.
Further, if a and b are any real numbers, then │a – b│ =│b – a│.
Again, absolute value is concerned with distance, not direction.
If we have two points on a line with coordinates a = 2 and b = 6, then the distance between them is
For example, solve the equation │3x + 5│= 20.
To solve the equation, set what is inside the absolute value sign equal to 20 and –20 and solve.
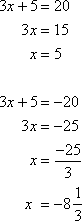
When we combine two inequalities using and or or, we get a compound inequality. When we combine them using and, both inequalities must be true. That is, any solutions must solve both inequalities. This is called a conjunction. When we combine using or, a solution is valid if it solves either inequality. That is, a valid solution may solve only one inequality. This is called a disjunction.
The following five theorems are used for dealing with inequalities containing absolute values. Most of these theorems can only be applied for positive numbers. However, theorem 1 can also be applied for zero.
For real numbers a > 0 and all real numbers x,
1. │x│ = a if and only if x = a and x = –a.
2. │x│ ![]() a if and only if –a
a if and only if –a ![]() x
x ![]() a.
a.
3. │x│![]() a if and only if –a
a if and only if –a ![]() x
x ![]() a.
a.
4. │x│ ![]() a if and only if x
a if and only if x ![]() a or x
a or x ![]() –a.
–a.
5. │x│ ![]() a if and only if x
a if and only if x ![]() a or x
a or x ![]() –a.
–a.
What is the value of x in the inequality │x│ ![]() 8?
8?
The correct answer is B . To solve, apply theorem 2.
–8 ![]() x
x ![]() 8
8
The solution set is {x│-8 ![]() x
x ![]() 8 } . This is a conjunction; to satisfy the inequality, x must be less than 8 and greater than –8.
8 } . This is a conjunction; to satisfy the inequality, x must be less than 8 and greater than –8.
What is the value of x in the inequality │x│![]() 15?
15?
The correct answer is D. To solve, apply theorem 5. Set x greater than or equal to 15 or less than or equal to –15. This forms the disjunction x ![]() 15 or x
15 or x ![]() –15.
–15.
In one last example, solve 54 ![]() │6x – 18│ for x.
│6x – 18│ for x.
To solve, apply theorem 3. Form the conjunction –54 ![]() 6x – 18
6x – 18 ![]() 54, and then solve.
54, and then solve.
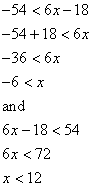
The solution is ![]() .
.