⬅ Previous Lesson Workshop Index Next Lesson ➡

Complex Numbers

Objective

In this lesson you will study how to graph complex numbers in the plane and perform operations with complex numbers.

Previously Covered:

The real numbers are the field of all rational and irrational numbers.

What are complex numbers?

What are complex numbers?

An imaginary number is the square root of a negative number. A complex number is the field of numbers in the form , which is called the standard form of the complex number, where a and b are real numbers and i is an imaginary number equal to . In the standard form of the complex number, a is the real part of the complex number and bi is the imaginary part.

A conjugate is created by changing the sign of the imaginary part of a complex number.

How do I perform operations with complex numbers?

We will study four operations with complex numbers:

(1) addition,
(2) subtraction,
(3) multiplication, and
(4) division.

First Operation—Addition

To add complex numbers, add the real parts and then add the imaginary parts. For example,

Question

Which choice shows the correct simplification of ?

Reveal Answer

The correct answer is D. To simplify, add the real parts, add the imaginary parts and then combine both parts.

Second Operation—Subtraction

Subtraction works in much the same way as addition. To simplify, subtract the real parts, and then subtract the imaginary parts. For example,

Question

Which choice shows the correct result of subtracting ?

Reveal Answer

The correct answer is A. To simplify, subtract the real parts, subtract the imaginary parts, and then combine the two.

Third Operation—Multiplication

Multiplication can be done using the FOIL method discussed earlier. For example,

Mathematically , so . Combine like terms for a final answer of .

Important Tidbit

It’s helpful to memorize the following:

Question

Which choice shows the correct simplification of ?

Reveal Answer

The correct answer is B. To simplify, use the FOIL method.

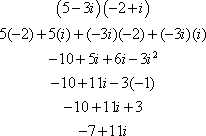
Fourth Operation—Division

To divide complex numbers, multiply by the conjugate of the denominator. For example, divide . The conjugate of the denominator is . Multiply the numerator and denominator by the conjugate, which will guarantee that you are multiplying by a form of one and not changing the value of the expression, to get . Use the FOIL method to multiply the numerators.

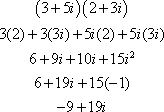
Then use the FOIL method to multiply the denominators.

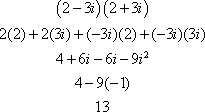
Finally, write the numerator over the denominator.

Question

Which choice shows the correct simplification of ?

Reveal Answer

The correct answer is A. To simplify, multiply the numerator and denominator by the conjugate, .

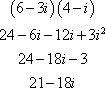
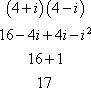
Finally, place the numerator over the denominator.

How do I graph complex numbers?

Each point (a, b) represents the complex number in the complex plane. The real axis is the horizontal axis and the imaginary axis is the vertical axis. For example, to plot the point , move 3 right and 2 up from the origin.

Question

Which point is shown on the graph?

Reveal Answer

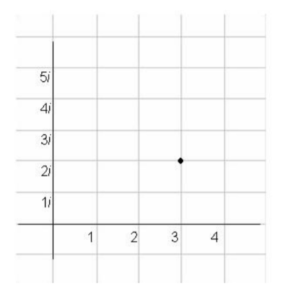
The correct answer is A. The real number axis is the horizontal axis and the imaginary axis is the vertical axis. The point shown is .

Review of New Vocabulary and Concepts

Like terms have the same variable raised to the same exponent.
Monomials can be added if they are like terms.
Monomials can be multiplied regardless of their variables and exponents.
Binomials can be added or subtracted by combining like terms.
One way to multiply binomials is to use the FOIL method.
To multiply polynomials, multiply each term in the first polynomial by each term in the second polynomial.
A complex number is the field of numbers in the form where a and b are real numbers and i is an imaginary number equal to .
To add complex numbers, add the real parts and then add the imaginary parts.
To subtract complex numbers, subtract the real parts and then subtract the imaginary parts.
To multiply complex numbers, use the FOIL method.
To divide complex numbers, multiply by the conjugate of the denominator.
To graph complex numbers in the plane, the real part is graphed on the horizontal axis and the imaginary part is graphed on the vertical axis.

⬅ Previous Lesson Workshop Index Next Lesson ➡