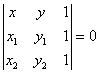username@email.com
username@email.com
In this lesson, you will compare symbolic and geometric interpretations of matrices. You will also infer geometric interpretations of the determinants of and matrices.
Consider a system of two-variable linear equations:
Similarly, in a system of three-variable linear equations:
Below is a system of two-variable linear equations with one solution.
When a system of two-variable equations has a solution, each equation can be graphed as a line. The solution set is the coordinates of the point where the two lines cross.
Solving the System
By Algebraic Symbols
By Matrices
y – 2x = 4
– (y + x = – 5 )
– 3x = 9
x = – 3
y – 2(– 3) = 4
y = – 2
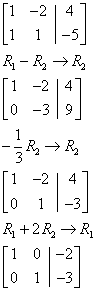
Solving the system results in the point (–3, –2).
If a system of equations has no solution, it is called inconsistent.
For example, 
, and 
.
The two lines defined by the equations are parallel. Because they never meet, there is no solution to the system of equations. An inconsistent system can be recognized by manipulating the system, and finding the result to be an inconsistent statement. In this case, the solution process yields the inconsistent statement
Solving the System
By Algebraic Symbols
By Matrices
2x + 3y = – 3
y =
.
2x + 3y = – 3
2x + 3y = 6
– (2x + 3y = 6)
0 = –9
This system is called inconsistent because both equations cannot be true at the same time.
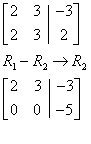
Notice that an inconsistent system in two variables indicates two lines that are parallel since the bottom row doesn’t have a one in it.
How does a system of two-variable linear equations with an infinite number of solutions relate to graphing?
If a system of equations has an infinite number of solutions, it is said to be redundant.
5x – 2y = 7
15x – 6y = 21
The graph of the line is purple in order to indicate that the red and the blue lines are the same. This system is redundant because both equations yield the same information—the same points. There are an infinite number of solutions to this system.
The two lines defined by the equations are the same line. Because they meet everywhere, there are an infinite number of solutions to this system of equations. A redundant system can be recognized symbolically by manipulating the system, and finding the result to be a universally true statement. In this case, the solution process yields the universally true statement
0 = 0, or 0x + 0y = 0.
Solving the System
By Algebraic Symbols
5x – 2y = 7
15x – 6y = 21
–3(5x – 2y = 7)
15x – 6y = 21
0 = 0
This system is called redundant because both equations yield the same information.
The solution can be characterized as
x = any real number and y =
.
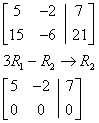
Notice that a redundant system in two variables indicates both lines are the same—that both equations describe the same relationship.
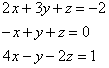
In this system, the three planes described by the equations meet at one point. (Think about the corner of a room or the vertex of a triangular pyramid.) Because there is one solution, the graph of the solution is a point.
Solution of System by Using Matrices
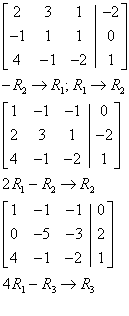
Go to column 2.
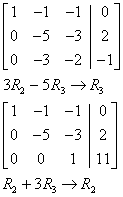
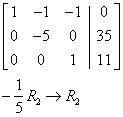
Go to column 3.
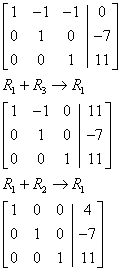
Solution:
x = 4
y = – 7
z = 11
How do you graph a system of three-variable linear equations with no solution?
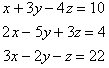
This system has no solution. Therefore, the graph will show three planes that never meet at the same place. For example, the three walls of a triangular room meet in pairs, but all three planes never meet simultaneously. This system is inconsistent.
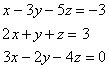
This system has an infinite number of solutions. Therefore, the graph of the solution is the line where two planes meet. This system is redundant.
Solution of System by Matrices
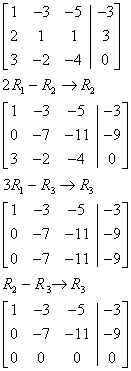
The final matrix has a row of all zeros. From elementary linear algebra we know that we need at least 3 equations to solve for 3 variables. Each row in the matrix corresponds to one of our equations, and the row of all zeros corresponds to an equation from which we get no information. Therefore, we only have two potentially useful equations, and we cannot solve for 3 variables with only two equations. As long as the remaining two rows are not inconsistent (in this case they are not, but we need to check!), the entire system is redundant. If the remaining two rows were inconsistent, the entire system would be inconsistent.
To represent the solution set, let z be any real number, and solve for the other two variables in terms of z.
z = any real number.
–7y –
11 z = –9
x – 3y
– 5z = – 3
Thus, if z is arbitrarily chosen as – 3, then 
and y = 6.
Or if z is arbitrarily chosen as 4, then 
and y = –5.
| Geometric Interpretations | |||
|---|---|---|---|
|
Number of Variables in the Linear System
|
One Solution
|
No Solution
|
Infinite Number of Solutions
|
|
2
|
Equations meet at a point. Graph shows two lines
that cross. |
Equations do not meet. Graph shows two parallel
lines. |
Equations yield the same relationship. Graph shows
the two lines coincide. |
|
3
|
Equations meet at a point. Graph shows three
planes that meet in one location. |
Equations do not all three meet. Graph shows
planes that do not meet simultaneously. |
At least one pair of equations is redundant. Graph
shows at least two planes that meet at a line. |
If the following is a reduced matrix form of a system of linear equations, how many solutions are there?
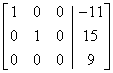
The correct choice is A. The final row indicates that 0x + 0y + 0z = 9, which is impossible. Thus there are no solutions.
If the following is a matrix form of a system of linear equations, what does the geometric representation look like?
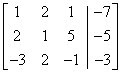
The correct choice is B. Rewriting the matrix in reduced-row echelon form yields:
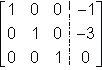
Therefore, the common solution for the system of equations is (x,y,z)=(-1,-3,0). That coordinate, alone, is shared by all three equations. Note that equations containing three unknowns indicate three-dimensional figures, in this case planes.
Suppose you have the matrix below.
This combination can be viewed as the two vectors [3, 0] and [1, 1].
Notice that the two vectors describe a parallelogram.
This parallelogram has a height of 1 and a width of 3. Thus its area is 1(3) = 3.
Notice that the determinant of our matrix is 3(1) – 1(0) = 3.
Suppose you have a triangle with vertices at 
. The area of the triangle can be determined by finding a determinant. The area is the absolute value of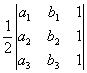 
. Note: the area must be positive, thus the absolute value of the expression is imperative.
What is the area of a triangle with vertices of (3, 1), (4, –7), and (0, –1)?
square units
square unitsThe correct choice is C. The solution is the absolute value of
.
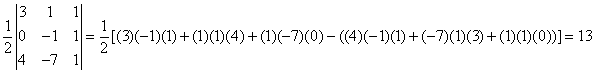Can determinants identify colinearity?
It follows from the triangle relation that if and only if three points 
are collinear, then
.
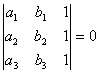Which is a value for x such that the three points (x, 1), (8, 4), and (–2, x – 5) are collinear?
The correct choice is D. There are two solutions to this problem: 3 and 14. Using the determinant method,
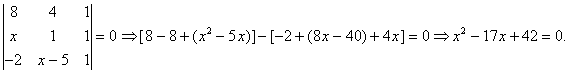
The quadratic equation 
has solutions of 3 and 14.
Can the equation of a line be found with determinants?
A line can be identified using two points 
. Using a generic point (x, y), the equation of a
line can be found using the following determinant equation.
