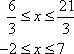username@email.com
username@email.com
In this lesson, you will study how to solve linear equations and inequalities.
A linear equation is an equation that can be written in the form ax + b = 0, where a and b are real numbers and a ≠ 0.
An equation is a statement showing that two mathematical expressions are equal. Thus, the following are equations.
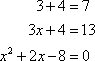
An equation in the form ax + b = 0 is a linear equation in one variable. It is also called a first-degree equation in one variable.
If an equation has no solution, it is called a contradiction.
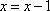
Equations that are true for all values of x are called identities.
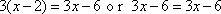
If an equation is true for a finite number of values for x, it is called a conditional equation.
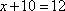
A conditional linear equation has exactly one solution.
To solve a linear equation, manipulate the terms until x is isolated on one side. To do so, follow these
steps.
1. Addition Property of Equality If a = b, then 
.
2. Subtraction Property of Equality If a = b, then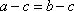 
.
3. Multiplication Property of Equality If a = b, then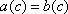 
, when c ≠ 0.
4. Division Property of Equality If a = b,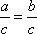 
, when c ≠ 0.
The properties of equality are true for all real numbers a, b, and c.
Which choice shows the solution to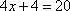 
?
The correct answer is A. To solve, first apply the subtraction property of equality.
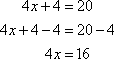
Then apply the division property.
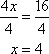
Which choice shows the solution to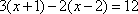 
?
The correct answer is B. To solve, first multiply to remove the parentheses, then combine like terms and simplify.
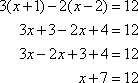
Then apply the subtraction property of equality.
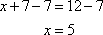
Use the same procedure and properties as before to isolate x on one side of the equation.
Which choice shows the value of x in the equation 
?
The correct answer is C. To solve, first remove the parentheses by distributing.
Then apply the subtraction property of equality, with the 3x term, and then the 3.
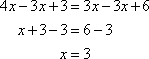
If there is a fractional coefficient in the problem, multiply by the lowest common denominator if possible.
Which choice shows the value of x in the equation 
?
The correct answer is D. To solve, first multiply both sides by the lowest common denominator.
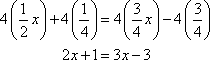
Then apply the addition property of equality.
Finally, apply the subtraction property of equality.
Inequalities are solved in the same way as equations. In inequalities, however, pay attention to the sign. The symbol > means greater than. The symbol < means less than. The symbol ≥ means greater than or equal to. The symbol ≤ means less than or equal to. Inequalities contain these symbols. The following are properties of inequalities, for all real numbers a, b, and c.
If a < b, then b > a.
If a < b and b < c, then a < c.
If a < b, then a + c < b + c.
If a < b, then a – c < b – c.
If a <b and c > 0, then a(c) < b(c).
If a < b and c < 0, then a(c) > b(c).
If a < b and c > 0, then 
.
If a < b and c < 0, then 
.
Note that there are two multiplication and two division properties. The order of an inequality reverses if both sides are multiplied or divided by a negative number.
Which choice shows the value of x in 5x + 3 > 2(x + 3)?
The correct answer is A. To solve, first remove parentheses by distributing, and then combine like terms.
Then apply the subtraction property of inequality.
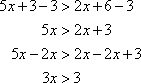
Finally, apply the positive division property.
The previous example showed an inequality in two parts: the left side and the right side. Inequalities can also have three parts: a left side, a right side, and a middle.
Which choice shows the value of x in 
?
The correct answer is B. To solve, first apply the subtraction property of inequality.
Then apply the positive division property.
