Your Dashboard username@email.com
⬅ Previous Lesson Workshop Index Next Lesson ➡

Matrices—Operations and Inverses

Objective

In this lesson, you will review matrices and their operations. You will also identify the properties of operations on matrices and explore inverses.

Previously Covered:

Matrices

  • A matrix is a rectangular array of numbers. The numbers in a matrix are referred to as the elements of a matrix.
  • A matrix is made up of rows and columns.The dimensions of the matrix are said to be “m by n” which is written .
  • An  matrix has m rows and n columns. This notation does not mean that you multiply m by n.
  • A matrix is sometimes called a row vector.
  • A matrix is sometimes called a column vector.
  • Let
  • A is a matrix, while both B and C are matrices.
  • The number 2 is the entry for a11, b21, b22, and c12.
  • Two matrices A and B are equal if A and B have the same dimensions, and every entry aij is equal to every entry bij.
  • The two matrices P and Q shown below are equal. Notice that they are both matrices and their respective entries are equal to each other.

How do you add and subtract matrices?

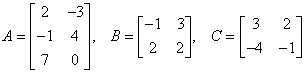
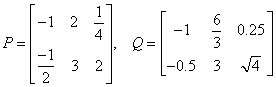
There are no surprises in addition and subtraction of matrices, however there is one requirement. The matrices must have the same dimensions. Once you establish that the matrices you are working with have the same dimensions, you can add or subtract each entry in the first matrix with the corresponding entry in the second matrix.

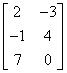
The sum and the difference of matrices B and C are shown below.

Question

Let .
What is J + K – L?

Reveal Answer

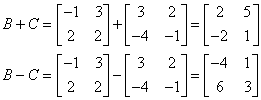
The correct choice is B. Add each entry ij of J to the respective entry ij of K, and subtract the respective entry ij of L.

Question

What are the dimensions of the matrix J in the example above?

  1. –2
  2. 8

Reveal Answer

The correct choice is D. The dimensions of a matrix are the number of rows by the number of columns.

How do you multiply with matrices?

There are two kinds of multiplication with matrices: scalar multiplication and multiplication of matrices.

Scalar multiplication changes the size of every entry by the same factor, called a scalar. A matrix of any dimensions may be multiplied by any scalar. Consider the scalar r = 3 and matrix . If we multiply these together we find:

rA = r

= 3=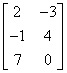

Matrix multiplication is more complicated. Not every pair of matrices can be multiplied. An  matrix can be multiplied only by an  matrix. This means that the number of columns of the first matrix must be the same as the number of rows of the second matrix. If the first matrix has dimensions , and is multiplied by a second matrix of dimensions , then the dimensions of the product matrix will be .

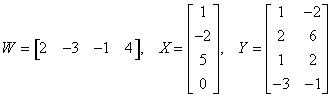
The product WX will have dimensions .

The product XW will have dimensions .

The product WY will have dimensions 

The product YW cannot be determined because the number of columns of Y is not equal to the number of rows of W. The product YW is not defined.

 

Multiplying Matrices

To find the product of AB: Each entry in the product matrix is a sum of the products of each entry in row i of A multiplied by the corresponding entry of column j of B. More precisely:

If ,

then AB = .

Question

What is the product GH, where

?

Reveal Answer

The correct choice is D.

Question

What is ST + P, where

?

Reveal Answer

The correct choice is B.

Question

What is , where A = ?

Reveal Answer

The correct choice is A.

Question

What is 2BA + C2, where A =
?

Reveal Answer

The correct choice is B.

Question

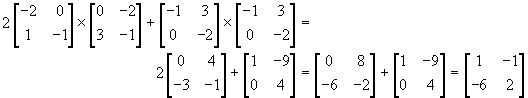
What is 3GH, where G = ?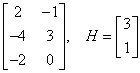

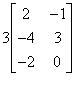
Reveal Answer

The correct choice is B.

Identity Matrix

When adding, an identity matrix is a matrix whose entries are all zeroes. This identity matrix is denoted O. Some examples are as follows:

When multiplying, an identity matrix is a matrix whose entries are all zeroes, except for the entries that lie on the main diagonal (top left to bottom right). The entries on the main diagonal are all ones. The identity matrix for multiplication is denoted I. Some examples are as follows.

How do you divide matrices?

Instead of division, matrix algebra focuses on using the multiplicative inverse of a matrix. The inverse of A, denoted by A–1, is the matrix that makes the expression below true.

Important Tidbit

In order to have an inverse, a matrix must be square. Not all square
matrices have an inverse.

For example, let T = . To find T–1, solve the following:

.

This means:

–2a + 3c = 1 –2b + 3d = 0 a – 2c = 0 b – 2d = 1,

a = –2, b = –3, c = –1, and d = –2.

Thus,
.

In fact, the inverse of a square matrix can be described by

, where ad – bc 0.

For the square matrix above, the value ad – bc is called the determinant. A matrix is invertible only if its determinant is non-zero. Determinants for larger matrices are discussed in another unit.

Properties of Matrix Algebra

Addition

Multiplication
Associative Property Yes Yes
Commutative Property Yes No
Identity A matrix in which all entries are zero. This matrix is denoted O. A square matrix in which all entries are zero except the entries on the diagonal from
a11 to ann , which has entries of 1. This matrix is denoted I.
Inverses The inverse of A is the scalar product of –1(A). Only some matrices have inverses.

Review of New Vocabulary and Concepts

  • A matrix is a rectangular array of numbers. Matrices can be added, subtracted, and multiplied.
  • The associative property exists in both addition and multiplication of matrices.
  • The commutative property exists only in matrix addition.
  • There are identity matrices in both addition and multiplication.
  • Every matrix has an additive inverse.
  • Only square matrices have multiplicative inverses.
  • Not all square matrices have multiplicative inverses.

⬅ Previous Lesson Workshop Index Next Lesson ➡

Back to Top