In this lesson, you will study how to solve systems of equations by graphing and substitution.
What are systems of equations?
An ordered pair (x, y) is the solution of a linear equation in two variables. A linear equation may be graphed using two points or one point and the slope.
A set of two or more linear equations with the same variables is a system of linear equations. Sometimes these are called simultaneous equations.
If there are two equations and two variables, the set of all ordered pairs that make both of the equations true is the solution set. If there are three variables and three equations, each solution is an ordered triple, such as (2, 4, 6).
When you solve a system of equations, you are finding the values for the variables that make all the equations true. If there is at least one solution to the system, it is called a consistent system. If there are an infinite number of solutions, the system is consistent and the equations are called dependent equations. If the system has no solution, it is called an inconsistent system.
How do we use graphing to solve systems of equations?
To solve a system of equations by graphing, we graph all the equations on a coordinate plane and find the point of intersection.
For example, solve the following system of equations by graphing:
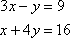 To graph these equations, we first solve for y, thereby putting the equations into slope-intercept form. The coefficient of x will be the slope and the constant will be the y-intercept.
To graph these equations, we first solve for y, thereby putting the equations into slope-intercept form. The coefficient of x will be the slope and the constant will be the y-intercept.
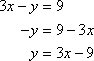 The slope of the first line is 3, and the y-intercept is at the point (0, –9).
The slope of the first line is 3, and the y-intercept is at the point (0, –9).
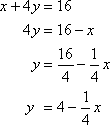 The slope of this line is
The slope of this line is 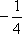 and the y-intercept is at (0, 4).
and the y-intercept is at (0, 4).
Graph these lines by plotting the y-intercept and then using the slope to find another point.
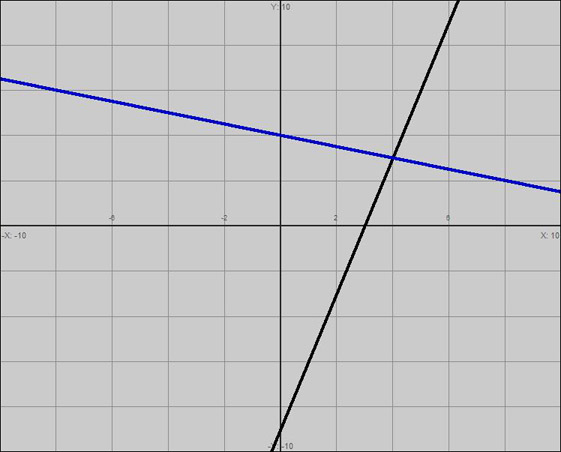 The lines appear to intersect around the point (4, 3). To see if we have solved the system, substitute these values back into the original equations to see if they make the equations true.
The lines appear to intersect around the point (4, 3). To see if we have solved the system, substitute these values back into the original equations to see if they make the equations true.
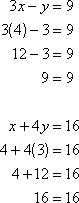 Though this method accurately solved these equations, graphing is not generally a very accurate way to solve systems of equations.
Though this method accurately solved these equations, graphing is not generally a very accurate way to solve systems of equations.
How do we use substitution to solve systems of equations?
A second, more accurate way to solve systems of equations is to use substitution. To do this, we follow the following procedure.
Step 1: Solve one of the equations for one of the variables. This will give us the value of one variable in terms of another.
Step 2: Substitute the expression we found for that variable into the other equation.
Step 3: Solve the equation into which the expression has been substituted.
Step 4: Using the value obtained, solve the first equation.
For example, solve the following system of equations by substitution.
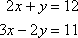 The first equation already has y without a coefficient, so it will be easy to solve for y.
The first equation already has y without a coefficient, so it will be easy to solve for y.
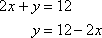 Then substitute 12 – 2x for y in the second equation and solve for x.
Then substitute 12 – 2x for y in the second equation and solve for x.
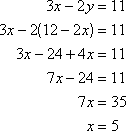 Finally, substitute 5 for x in the first equation.
Finally, substitute 5 for x in the first equation.
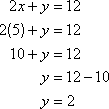 The ordered pair (5, 2) solves both equations, and you can check by substituting into the original equations if you want to.
The ordered pair (5, 2) solves both equations, and you can check by substituting into the original equations if you want to.
Review of New Vocabulary and Concepts
- A relation is a rule or mapping between elements of two sets, a set of ordered pairs, or an equation or inequality in two variables.
- A function is a relation in which each element of the domain corresponds to one and only one element in the range.
- A linear function is in the form ƒ(x) = mx + b.
- A composite function combines functions in a specific order. A composite function is denoted as ƒ(g(x)) is (ƒ ο g)
- An inverse function exists when the domain and range of a function are interchanged and the result is a new function. An inverse function is denoted ƒ –1(x). Inverse functions undo each other.
- A sequence is an ordered set of numbers that are related mathematically. Each value in a sequence is called a term. The nth term is the general term. For example, the natural numbers that satisfy ƒ(x) = 2n – 1 constitute a sequence.
- A rule for finding the terms in a sequence by operating on the previous term is called a recursive formula.
- An explicit formula enables us to find a term without knowing the previous term.
- The sum of terms in an arithmetic sequence is called an arithmetic series. We use the Greek letter sigma (
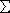 ) to write a series in series notation.
) to write a series in series notation.
- In a geometric sequence, there is a common ratio between any two consecutive terms.
- The formula for the nth term, or common term, of a geometric sequence is an = a1r n – 1 , for all n
 1, where r is the common ratio, a 1 is the first term in the sequence, and an is the common term.
1, where r is the common ratio, a 1 is the first term in the sequence, and an is the common term.
- A linear equation can be written in the form ax + b = 0.
- Linear inequalities use the symbols
 (greater than),
(greater than),  (less than),
(less than), 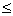 (less than or equal to), or
(less than or equal to), or 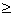 (greater than or equal to).
(greater than or equal to).
- The slope-intercept form of an equation for a line is y = mx + b.
- Graphing an inequality divides the coordinate plane or Cartesian plane into two half-planes. If the inequality contains
 or
or  it is graphed using a broken line. If it contains
it is graphed using a broken line. If it contains 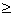 or
or 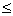 , it is graphed using a solid line.
, it is graphed using a solid line.
- Parallel lines are lines in the same plane that do not intersect.
- Two lines are perpendicular if their intersection forms four right angles.
- The absolute value of a number is its distance from zero on a number line. Absolute value is always positive.
- A set of two or more linear equations is a system of equations.
 username@email.com
username@email.com
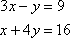
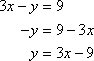
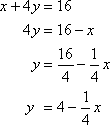
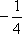 and the y-intercept is at (0, 4).
and the y-intercept is at (0, 4).

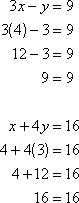
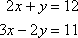
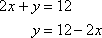
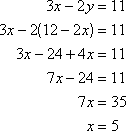
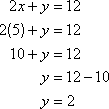
 ) to write a series in series notation.
) to write a series in series notation. 1, where r is the common ratio, a 1 is the first term in the sequence, and an is the common term.
1, where r is the common ratio, a 1 is the first term in the sequence, and an is the common term. (greater than),
(greater than),  (less than),
(less than), 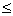 (less than or equal to), or
(less than or equal to), or 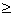 (greater than or equal to).
(greater than or equal to). or
or  it is graphed using a broken line. If it contains
it is graphed using a broken line. If it contains 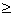 or
or 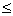 , it is graphed using a solid line.
, it is graphed using a solid line.